шив при этом запас устойчивости. В обобщенных квадратичных оценках /21. накладывают ограничение не только на величину отклонения е (t), но и на скорость отклонения е {t) в а также и на производные второго, третьего и высших порядков в J22, J2n, что означает приближение кривой не к ступенчатой функций, а к экспоненте в случае /21 и к более плавной, но сложной кривой в случае использования /22. Jan-.ripn выборе параметров САУ по минимуму /21.

Jn существен выбор постоянных т, т , определяющих вес производных в обобщенных квадратичных оценках (4.58), (4.59). Значительное увеличение т, т приводит к отсутствию перерегулирования, но увеличивает время регулирования. При малых Tl, Тп уменьшение колебательности будет незначительным. Выбор Ту, т осуществляется с учетом постоянной времени экстремали, к которой целесообразно приближать процесс.

Остановимся на методике расчета- системы по минимуму обобщенной квадратичной оценки:

Л1 = [бв(0 + т?ев(0]й.

Этот интеграл можно представить в виде суммы двух интегралов:

оо оо

Л1 = j [есв (О + Tl ёсв (01 dt- 2ti j е (t) ёсв (t) dt = о о

-1 [есв it) + Tl еов (01 dt - 2ti e (0 db (0-0 0

Если система устойчива, то lim Есв (О = 0. тогда

2x11 есв (О deoB (О = Ч е?в (О J = е?е (0). о о

Кроме того, интеграл /21 будет иметь минимально возможное значение

J2! ,in=Ti8eo(0) (4.66)

еев(0+Т1ё,в(0=0. (4.67)

Если

то решение дифференциального уравнения (4.68) еев(0=еев(0)е-/.

(4.68)

(4.69)

является оптимальным по минимуму (экстремальным) переходным процессом (где - постоянная времени этого процесса).

При выборе парамегров системы по минимуму J обычно имеет место агклонение /Jimin от наименьшего значения

.21т1гч

Т. е. /Ilmin - /

== б>0.

А. А. Фельдбаумом [10] было показано, что переходный процесс будет отличаться от экстремального на величину, меньшую Yblx, т. е.

Абев(0<Кб7 (4.70)

По величине б можно оценить отклонение истинного переходного процесса ев (О от экстремального (рис. 4.22). При увеличении порядка системы увеличивается и ширина зоны ±УЫх, при этом уменьшается точность оценки качества системы (приближения переходного процесса к экстремали); во избежание этого используют оценки вида (4.59). Величину задают по требуемому времени регулирования t, т. е. ?р/6 < Ti < ?р/3.

Следует заметить, чго задача выбора параметров по минимуму /го или /г! решается аналитически лишь в несложных случаях для САУ невысокого порядка. В про- св тивном случае расчеты существенно усложняются и задачу следуег решать численно на ЦВМ.

Рассмотрим примеры выбора оптимального значения какого-либо параметра системы по минимуму /го и /гх.

Пример 4.4. Вычислить значение коэффициента

усиления системы, миии- Рис. 4.22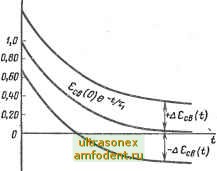

мизирующее квадратичную интегральную оценку J Известна передаточная, функция разомкнутой системы

. W(s) = ft/Is (1 + sT,) (1 + sTh

где Tl = 0,01 с; Т = 0,03 с.

Входной сигнал - единичная функция g (t) = Л (О-Изображение отклонения г (О по Лапласу

Е = -(л 1 si\+sTi)(\+sT,) s S y + W(s) S s(\+sTi){\+sT)+k

T,T+s(Ti + T)+\ bps+bys+bl

где 6o=o:o = r, Гз = 3-10-*; b, == о, = Ti + = 4-10-; 6j=ag=rl;

Воспользуемся формулами для вычисления Jjo, приведенными в табл. 4.1 для п = 3:

J Ь Яр 1 + {Ь\ - 2fco йд) Со Сз + fcg Да Дз 2оо Дз (дл 2 - о Оз)

До Д1-Дрal-alk 1 k (а\ - Др) + а,

~ -fe22ag + fe2apo, 2 ка-кОо

Определим частную производную:

dJjB 1 (flf - Др) (fli - feop) - [fe (д? - Др) + Д1] (Д1 - 2др к)

дк ~ 2 kiai-kao)

Определим k из dJ2o/dk=0, т.е. яр (of - йо) + 2яо Oi fe-of =0. Подставляя числовые значения коэффициентов, получим

fei* + fe 61,5 - 41- 10* = О,

откуда feonx ~ 37.

Пример 4.5. Определить оптимальное значение коэффициента усиления fe, соответствующее минимуму обобщенной квадратичной оценки

Передаточная функция разомкнутой системы W (s) = fe/s (1 + + sT)]; 7 = 0,1 с; т = 0,5 с.

Входной сигнал - единичная функция g = 1 (t). Можно представить J21 в виде суммы:

оо оо оо

У2,= [е1в(П + ё?в(0] d<= J <B{t)dt + x J ilAOdt-