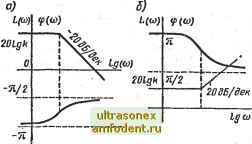Рис. 2.11

ни уравнения R (s) - О, т. е. такие значения s, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения Q (s) = О, т. е. такие значения s, при которых передаточная функция обращается в бесконечность.

Все рассмотренные выше алементарные звенья относятся к минимально-фазовым. Примерами неминимально-фазовых элементарных звеньев являются звенья с передаточными функциями:

W is) = k/iTs - 1); W {s)k(Ts- I); W (s) = ft/(rV-

-2lTs + 1); W (s) = k (Ts - 26rs + 1)

и др. Для неминимально-фазового звена характерно, что у него сдвиг фазы по модулю больше, чем у минимально-фазового звена, имекщего одинаковую с неминимально-фазовым звеном АЧХ.

На рис. 2. И приведены ЛЧХ неминимально-фазовых звеньев с передаточными функциями W (s) = 1/(Г5- 1) (рнс. 2.П, а), и W (s) = ft (Ts - 1) (рис. 2.11, б). ЛАЧХ этих звеньев совпадают с ЛАЧХ апериодического (см. рис. 2.7, б) и форсирующего (см. рис. 2.8, б) звеньев. Сдвиг фазы у последних меньше: фазовые частотные функции апериодического и форсирующего звеньев по абсолютной величине не превышают значения я/2, а фазовые частотные функции соответствующих неминимально-фазовых звеньев достигают по абсолютной величине значения я. К неминимально-фазовым звеньям относят также звено чистого запаздывания с передаточной функцией W (s) = fte-

Частотная передаточная функция

W (/сй) fte - = ft (cos сот --/ sin ют).

Рис. 2.12

Для оета.льных частотных и временных функций имеем:

и {(6) = k cos tor; V (о) = -k sin tor; A (w) = k; чр (ю) = - ют; L (to) = 20 Ig k; h (t) = kl {t - т); w (t) =

= m {t - t).

Амплитудно-фазовая частотная характеристика (рис. 2.12, а) - окружность с центром в начале координат и радиусом k. Канадой точке этой характеристики соответствует бесконечное множество значений частот. ЛАЧХ (рис. 2.12, б) совпадает с ЛАЧХ пропорционального звена с передаточной функцией к, ЛФЧХ (рис. 2.12, б) - с графиком функции у = - х10* (у = Цсй); X == Igw). Переходная характеристика приведена на рис. 2.12, в.

§ 2.7. Структурные схемы, графы, уравнения и частотные характеристики стационарных линейных систем

Структурной схемой в теории автоматического управления называют графическое изображение математической модели автоматической системы управления в виде соединений звеньев. Звено на структурной схеме условно обозначают в виде прямоугольника с указанием входных и выходных величин, а также передаточной функции внутри него. Иногда вместо передаточной функции указывают уравнение или характеристику. Звенья могут быть пронумерованы и их передаточные функции, уравнения или характеристики представлены вне структурной схемы.

Входные и выходные величины записывают в виде изображений, если передаточные функции задают в форме изображений. Если же передаточные функции задают в операторной форме или звенья описывают дифференциальными уравнения-tiii, то входные и выходные переменные записывают в виде оригинала.

Сравнивающие (рис. 2.13, а, б) и суммирующие (рис. 2.13,в) звенья изображают в виде круга, разделенного на секторы. В сравнивающем звене сектор, на который подается вычитаемое , затемняют (рис. 2.13, б) или перед соответствующим входом ставят знак минус (рис. 2.13, а).

Структурную схему широко используют на практике при исследовании и проектировании автоматических систем управления, так как она дает наглядное представление о связях между звеньями, о прохождении и преобразовании сигналов в системе.

При математическом описании автоматическую систему обычно изображают в виде блок-схемы и для каждого блока (элемента) записывают уравнения, исходя из физических законов, которым подчиняются процессы в нем. Структурную схему можно составить на основании этой блок-схемы и полученных уравнений или только на основании последних. И дальнейшие преобразования, необходимые для получения уравнений и передаточных функций системы, проще и нагляднее производить по структурной схеме.

Звено на структурной схеме не обязательно изображает модель какого-либо отдельного элемента. Оно может быть моделью элемента, соединения элементов или вообще любой части системы.

Основные правила преобразования структурных схем.

1. Последовательное соединение звеньев (рис. 2.14, а). При последовательном соединении выходная величина каждого предшествующего звена является входным воздействием последующего звена. При преобразовании структурных схем цепочку из последовательно соединенных звеньев можно заменить одним звеном (рис.

2.14, б) с передаточной 5) в)

функцией W (s), равной у, /CNAj-y? tf,/ОчД-У; Ц/ОчУ-у.й, произведению передаточных функций отдельных

звеньев: W7(s)=nWj (.s).