

 |
 |
|
Главная страница Векторные методы процессов Тогда на основании метода суперпозиции установившаяся ошибка САУ е it) = eg (t) + Ef if). (4.9) где Eg it) - ошибка отработки системой задающего воздействия: a (/) - ошибка, вызванная действием помехи: Efit) = s=0 l+kikz В данном случае САУ является статической относительно обоих воздействий, так как eg (t) фО и {t) Ф 0. 2. Допустим, что в элемент 2 рассматриваемой системы (рис. 4.2) включено интегрирукицее звено, а элемент / является инерционным звеном, как и в случае 1. При этом передаточ-най функция элемента 2 (S) = kjb (1 + sTg)]. Тогда составляющие eg if) и if) ошибки системы (4.9) l+Vi?i(s)r,(s) 8(0 = s = 0 Lfti +8 (1 + sT-i) (1 +87-2) Js= 0 (s) 0=0; Ll+W7i(s)W7,(s) /0 - Следовательно, САУ является астатической относительно задающего воздействия g if) и статической относительно возмущения / it). 3. Пусть интегрирующее звено включено в элемент /, передаточная функция его при этом равна (s) = Vis (1 + s7i)l. Второе звено является инерционным звеном, а передаточная функция его та же, что и в случае 1. Рассчитаем составляющие ошибки &g (t) и (t): %(0 = s(l + sT,)(l+sT,) lkik,+s{l+sT,)(l+sT,)i .l-HlFi(s)W2(s) s(l+sri) Поскольку и Eg (/) и (t) = 0, система является астатической и относительно воздействия g (t), и относительно возмущения / (О- Нужно отметить, что метод коэффициентов ошибок применяется при сравнительно медленно меняющихся воздействиях. Пример 4.1. Для системы (рис. 4.1) определить значение установившейся лшибки системы. Передаточная функция системы в разомкнутом состоянии U7 (S) = Ms (1 + sTj) (l-b sT)], где fe = 10 c-i; Ti = 0,2 c; = 0,02 c. Выходной сигнал меняется по закону g {() - 5 + 2Qt + 20<. Найдем передаточную функцию замкнутой системы относительно ошибки: Е (S) G(s) s(l+sTy)(l+sT) Коэффициенты ошибок Q и (Co = 0, так как система астатическая) определяют по (4.7) или разложением в ряд по возрастающим степеням s функции W (s) делением числителя на знаменатель: Wge (s) =CiS-bCa +... s/k+s (Ty + T~\lk)lk+.....- Коэффициенты Cg, ... вычислять не имеет смысла, так как функция g (О имеет только две производные, ие равные нулю. Определим первую и вторую производные входного воздействия i(0==20-b40r, g(0=40. Тогда ев (О = Cj g (О -[- С g (<) = 2,48 -h 4<. § 4.3. Оценка качества переходного процесса при воздействии ступенчатой функции Переходный процесс в системе зависит не только от свойств САУ, но и от характера внешнего воздействия, которое в общем случае может быть сложной функцией времени. Поведение системы рассматривают при следующих типовых воздействиях: единичной ступенчатой функции 1 (t), импульсной 6 (О и гармонической функций. Прямые оценки качества получают по кривой переходной характеристики h (t), т. е. при воздействии единичной ступенчатой функции , = ,(0-( I о при /<0 и Нулевых начальных условиях. Эту характеристику можно построить для выходной величины или для отклонения всв (О (рис. 4.3, а, б). К прямым оценкам качества относят: 1. Время регулирования tp - минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью (4.10) Иев(01<0 при it где А - постоянная величина, значение которой нужно оговаривать (задается величина А в процентах от установившегося значения выходной величины h. 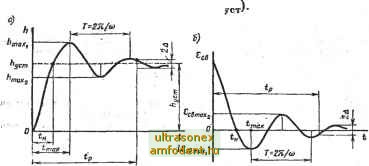
|
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |