рой наклон ЛАЧХ увеличивается на 20 дБ/дек, соответствует множитель (s/wj -f 1) в полиноме Q i (s). Сопрягающей частоте (Oj, при которой наклон ЛАЧХ уменьшается на 20 дБ/дек, соответствует множитель (s/idj -f 1) в полиноме (s). Если при какой-то частоте ©j или ©j- наклон ЛАЧХ изменяется на 40 дБ/дек, то ей соответствует квадрат указанного множителя.

Затем, пользуясь формулами (5.15), следует определить передаточные функции Wz и W 3 соответственно параллельного и прямого параллельного корректирующих устройств, эквивалентных требуемому последовательному корректирующему устройству. Если передаточная функция Wta сложная, то по формулам (5.17) целесообразно выяснить, при каких передаточных функциях Wki и Ws требуемое последовательное корректирующее устройство может быть заменено двумя корректирующими устройствами: последовательным и параллельным.

На основании полученных, результатов и физических свойств элементов неизменяемой части системы можно выбрать один из вариантов включения корректирующего устройства. При отсутствии очевидных и веских преимуществ одного или двух из возможных вариантов следует рассматривать все варианты.

По виду передаточной функции корректирующего устройства может быть выбрана схема пассивного четырехполюсника для реализации этой передаточной функции. Краткие сведения о пассивных четырехполюсниках даны в § 5.3. Более обширные сведения можно, например, получить в [7, 81.

Легко реализуются передаточные функции с полиномами

(s) и Q (s) первой и второй степеней. При более высокой степени этих полиномов следует использовать два пассивных четырехполюсника, соединенных последовательно. Основные соображения о такой возможности цзложены в § 5.3.

После выбора электрической схемы необходимо вычислить требуемые значения емкостей и сопротивлений и убедиться в возможности физического выполнения этой схемы с необходимыми параметрами ее передаточной функции. В частности, не следует предусматривать пассивный четырехполюсник с очень малым (менее 0,1-0,05) передаточным коэффициентом или с весьма большими емкостями. Не следует также иметь в одной схеме емкости (или сопротивления), значительно, на 2-3 порядка, отличающиеся друг от друга по величине.

Обычно требуемые значения параметров передаточной функции пассивного четырехполюсника можно иметь при нееколь-

ких вариантах значений его элементов. В корректирующих устройствах используют и активные четырехполюсники (см. § 5.3).

Следует указать на одно обстоятельство. Предположим, что параллельное корректирующее устройство (см. рис. 5.1, ё) охватывает участок цепи с астатизмом v-ro порядка, т. е. Wi = kRAs)/lsQ{s)l,

где Ri (s): Qi {s) - полиномы от s с равным единице свободным членом.

Корректирующее устройство не изменит порядок астатизма этого участка цепи, если его передаточная функция

WkRis)sVlQ{&n, (5Ла)

где /?к2 (s): Qk2 (s) - полиномы от s с равным единице свободным членом.

Действительно, при таком корректирующем устройстве передаточная функция рассматриваемого участка цепи

i + W Й7 , [Qj (S) Q 2 (s) + k. i?2 (s) Яъг (s) I T. e. астатизм участка остался прежним.

Заключительные этапы синтеза. При построении желаемой ЛАЧХ предполагалось что неизменяемая часть системы с усилителем имеет необходимый передаточный коэффициент. После выбора корректирующего устройства передаточный коэффициент разомкнутой системы, как правило, изменяется. И теперь нужно окончательно определить необходимое значение передаточного коэффициента усилителя. На этом синтез системы закончен.

Однако построение желаемой ЛАЧХ основано на определенных допущениях. Кроме того, 1огла иметь место приближенная реализация требуемой ЛАЧХ корректирующего устройства. Поэтому совершенно необходима проверка качества синтезированной системы. С этой целью строится переходная характеристика замкнутой системы и определяются показатели ее качества. Если система третьего порядка, то переходную характеристику удобнее строить операционным методом. Методика определения корней данного полинома изложена в начале данного параграфа. При более высоком порядке системы нужно пользоваться методом вещественных частотных характеристик (трапецеидальных или треугольных). При аппроксимации вещественной частотной характеристики отрезками прямых необходимо учитывать следующее: аппрок-

симацию начинать из начальной точки характеристики; при не слишком сложной форме характеристики достаточно заменить ее четырьмя-пятью трапециями (или треугольниками); хвост характеристики, т. е. ее конечный участок с ординатами менее О, 1 от начальной, можно отбросить.

При существенном невыполнении требований к системе - при перерегулировании и времени регулирования больше допустимых значений - необходимо выяснить и устранить причины неудачного решения.

Кроме ошибок в расчете могут быть неточной реализация требуемой передаточной функции коррректирующего устройства и недостаточным избыток фазы при контрольных частотах и cog.

Возможно также значительное отличие вещественной частотной характеристики синтезированной системы от типовой, для которой справедливы номограммы (см. рис. 5.24 и 5.25), положенные в основу расчета. В этом последнем случае рас-счет следует повторить, задавшись значениями а и меньше требуемых.

Пример 5.2. Регулируемый объект и исполнительный э.пемент при- борной следящей системы описываются передаточной функцией

Wo (s) = k/ls (0,005s + 1) (0,01 s +

Требуется выбрать последовательное корректирующее устройство, обеспечивающее при k = 200 с-* и v = 1 следующие показатели качества: а < 30% и <р < 0,5 с. Допустимое ускорение регулируемой координаты гг) = 50 рад/с при начальном рассогласовании =0,1 рад.

Прежде чем начать расчет, заметим, что при k = 200 система без корректирующего устройства неустойчива. Действительно, в этом случае ее характеристическое уравнение

+ 200 = О и определитель Гурвица CiCg - СоСз = 0,06 - -0,1 = - 0,04 < 0.

Расчет построения меняемой мы. При (о

ем ординату 20 Ig й = = 20 Ig 200 = 46 дБ; сопрягающие частоты (Oi = 1/0,05 = 20 С- : 2 = 1/0,01 = 100с-*. ЛАЧХ неизменяемой части системы Lq (w) состоит из трех асимптот Рис. 5.28 и построена на рис. 5.28.

0,0005s3 + 0,06 s -f s2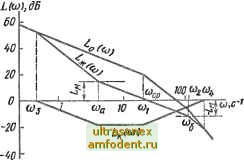

начинаем с ЛАЧХ неиз-части систе-= 1 вычисли-