диусом и сферу 6=2 xfo с радиусом V- Выберем радиус сферы е произвольно малым. Если невозмущенное движение устойчиво, то для этой сферы должна найтись другая сфера б, обладающая следующим свойством; изображающая точка УИ, начав свое движение из любой точки Мо, лежащей внутри или иа поверхности сферы б, при своем дальнейшем движении остается всегда внутри сферы е, никогда не достигая ее поверхности (рис. 3.3).

Если же невозмущениое движение неустойчиво, то траектория изображающей точки М с течением времени пересечет сферу е изнутри наружу (или попадет на ее поверхность) при сколь угодно близком положении точки Мо к началу координат.

Заметим, что при i > 3 надо рассматривать движение изображающей точки в многомерном пространстве относительно гиперповерхностей (гиперсфер) и рассмотрение теряет наглядность.

Практически устойчивость данного невозмущенного движения означает, что при достаточно малых начальных возмущениях возмущенное движение будет сколь угодно мало отличаться от невозмущенного движения. Если невозмущенное движение неустойчиво, то возмущенное движение будет отходить от него, как бы малы ни были начальные возмущения.

Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных возмущениях стремится к невозмущенному движению, т. е.

lim л;,-(0 = 0, (3.14)

то невозмущенное движение называют асимптотически устойчивым.

При асимптотической устойчивости изображающая точка с течением времени должна неограниченно стремиться к началу координат, не выходя из сферы е.

Отметим некоторые особенности определения устойчивости по А. М. Ляпунову. Во-первых, предполагают, что возмущения налагаются только на начальные условия, иначе говоря,

возмущенное движение происходит при тех же силах (источниках энергии), что и невозмущенное движение. Во-вторых, устойчивость рассматривают на бесконечно большом промежутке времени. В-третьих, возмущения предполагаются малыми. Несмотря на эти ограничения, определение А. М. Ляпунова устойчивости движения является эффективным и плодотвор-Рис. 3.3 ным в приложениях.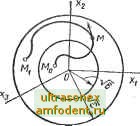

§ 3.3. Теорема А. М. Ляпунова об устойчивости движения по первому приближению

Когда известно общее решение дифференциальных уравнений движения (3.1), можно непосредственно определить значения переменных iji {t) в возмущенном движении, составить вариации Xi = t/j {t) - y*{t) и, исследуя их, решить вопрос об устойчивости невозмущенного движения у1 (t). Однако, как правило, исследование устойчивости движения производят не путем анализа общего решения, а методами, основанными на качественном анализе дифференциальных уравнений возмущенного движения, которым удовлетворяют отклонения (вариации) Xt.

Чтобы вывести уравнения возмущенного движения, найдем из (3.9) переменные yt (t) = yi (t) -f Xi(t) и подставим эти значения yt (t) в дифференциальные уравнения движения (3.1). Тогда

dynmt+-dXi(t)/dt = Yi{t/-t+Xx, уЬ-х, i/A-f л , t). (3.15)

Если йравые части уравнений (3.15) допускают разложение в степенные ряды Тейлора, то после этого разложения по степеням Xi получим

i + i.v .-......г., ..+...

- + (-)п+/?И1. .... an). (3.16),

где Ri {Xi, лга,..., Xji) --. совокупность членов, зависящих от отклонений Xi в степени выше первой. Учитывая (3.4), будем иметь

dXi(t)/dt = aiiXi + ai.,x + ...+ainXn + Ri(xi, х, Хп). (3.17)

В уравнениях (3.17) коэффициенты

(3.18)

В общем случае являются функциями времени t; в частности, они могут быть постоянными, в дальнейшем, если не будет оговорено особо, будем считать коэффициенты о.- постоянными.

Уравнения (3.17) называют дифференциальными уравнениями возмушенного движения.

Если отклонения л:,- достаточно малы, то, пренебрегая Riixi, лга, Хп), получим линеаризованные уравнения

aXi/dt=aiiXi + ai2X2 + ...+ai x , i = l, 2, п. (3.19)

называемые уравнениями первого приближения.

Во многих случаях устойчивость движения исследуют по уравнениям первого приближения. Это объясняется не только простотой этого метода, но также и тем, что знания процессов, происходящих в реальных системах, позволяют надежно определять только первые линейные члены. Однако на основании уравнений первого приближения можно дать иногда неверное заключение об устойчивости движения. Поэтому, естественно, возникает вопрос об определении условий, при выполнении которых по уравнениям первого приближения можно дать правильные ответы об устойчивости движения. Эту исключительно важную и принципиальную для теории автоматического управления задачу впервые поставил и решил А. М. Ляпунов.

Системе уравнений (3.19) соответствует характеристическое уравнение, которое можно записать следующим образом:

D(.s) =

21 22-5 - (hn

= 0. (3.20)

Из (3.20) можно найти его корни s,-, где i = 1, 2, .... п, которые в общем случаеимеют вид Sj = ± /сог, где а,- и (О; - вещественные и мнимые части корней соответственно.

Для исследования устойчивости систем по их линеаризованным уравнениям принципиально важны следующие теоремы А. М. Ляпунова, которые приведем без доказательства.

Теорема 1. Если вещественные части всех корней Si характеристического уравнения (3.20) первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.

Теорема 2. Если среди корней Si характеристического уравнения (3.20) первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.

Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то этот случай называют