ций дуг, входящих в этот путь; т - общее число таких путей; д - определитель графа;

Д = 1-S 0,- + 2 wo.- 2 0.- wo. woi -ь /.ft /.ft,/

где в первой сумме IFj-передаточная функция у-го простого контура, равная произведению передаточных функций входящих в этот контур дуг, и суммирование производится по всем простым контурам; во второй сумме IFoyWofe - произведение передаточных функций /-го и k-ro контуров и суммирование производится по всем несоприкасающимся парам контуров; в третьей сумме Wfj Wk oi - произведение передаточных функций /-го,/г-го и/-го контуров и суммирование производится повеем несоприкасающимся тройкам контуров и т. д.; Д,- - определитель подграфа, получающегося из исходного графа при удалении дуг и вершин i-ro простого пути, а также всех дуг, инцидентных этим вершинам.

Два контура (пара контуров) называются несоприкасающимися, если они не имеют общих дуг и (или) общих вершин. Тройка (четверка и т. д.) контуров называется несоприкасающейся, если любая пара контуров из этой тройки (четверки и т. д.) является несоприкасающейся.

Подграф, получающийся при удалении дуг и вершин какого-либо простого пути, а также всех дуг, инцидентных удаляемым вершинам, будем называть подграфом, соответствующим этому простому пути.

Граф на рис. 2.26, а имеет два простых пути от вершины g к вершине х (пунктирные линии с точками). Передаточные функции этих путей = WWW; = IFilF.. Он содержит пять простых контуров (см. замкнутые пунктирные линии) с передаточными функциями

= 14; Го-з = W, Wi., W W W;

Wo. = 122 №33 W. 13, W ; = 1з4

34Г3,.

и три несоприкасающиеся пары контуров с передаточными функциями Wot и Wos, Woi и IF04. Wi и 7о5-

Этот граф не содержит несоприкасающихся троек и большего числа контуров, поэтому определитель

Л = 1 - (IFoi + IFo, + lFo3 + Wo + Wo,) + (IToiX

X + Wor Wo, + IFo, Wo,).

Подграф, соответствующий первому простому пути (рис. 2.26, б), имеет один контур, а подграф, соответствующий второму простому пути (рис. 2.26, в), - два контура. Определители этих подграфов д1 = 1 - IFq-i; Л2 = 1 - (01 + 05) + + 101 Wo,.

Согласно формуле Мейсона. передаточная функция

Пример 2.5. Вычислим передаточные функции системы управления, рассмотренной в примере 2.4 (см. рис. 2.22, а). Граф этой системы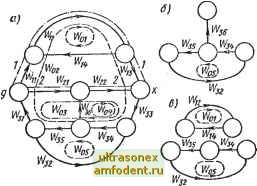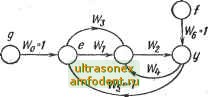

Рис. 2.27

управления приведен на рис. 2.27. Найдем передаточные функции Wyg, Wyf и Weg-От вершинЬ! g к вершине у имеется два простых пути с передаточными функциями U7i = Wo Wi = Wi U7,;

Имеется три контура с передаточными функциями йох- = U7i Wi Wb= -WiW; = WWi, Wo3= WgWWb = = -WWs.

. Несоприкасающихся пар и большего числа контуров граф не содержит. Поэтому его определитель

Л = I -(U7 -f Гоз) -l+W.W-W.Wt + WW,.

Подграфы, соответствующие простым путям от вершины g к вершине у, замкнутых контуров не содержат, и их определители Aj = 1,

А2 = 1-

По формуле Мёйсона,

Vlpg = (Wl+Wi)/A = (W,W + WW,)/{i+ U7, W -WW, + Гз)

От вершины f к вершине у ведет один простой путь - дуга ttg. Соответствующий этому пути подграф не имеет замкнутых контуров, и его определитель Aj = I. Следовательно,

Wyf = Гб/Д = 1 / (1 + U7i -WWi+Ws).

От вершины g к вершине е ведет также один простой путь - дуга W . Соответствующий этому пути подграф имеет один контур с передаточной функцией Woi = WWi, и его определитель Ai = 1 - ==

~ 1 - U2 W.

Передаточная функция

Weg = WoA,/A = (\-WW)/(\+WxW-WW, + WWs).

Дифференциальные уравнения. Зная передаточные функции системы, нетрудно записать ее дифференциальные уравнения. Если система имеет одну управляемую величину, то для ее полного описания достаточно иметь одно дифференциальное уравнение, выражающее зависимость между выходной и входной величинами.

Автоматические системы с одной управляемой величиной называют одномерными. В общем виде дифференциальное уравнение одномерной системы с двумя входными величинами, например задающим воздействием g и возмущающим воздействием /, можно записать как

in) <п-i) (т) <т-1)

cioy-\-ciiy + ... + a y = bog + big + .. + brng + <z)

+ cJ + cJ + ... + Cif.