Уравнение асимптотической ЛАЧХ имеет вид

20 Ig k при со < ©i;

20 Ig k -40 Ig Тсо при со > coi,

где coi = \IT является сопрягающей частотой. Оно получается из уравнения (2.51), если под корнем при со < со оставить только единицу, а при сосо - слагаемое Г*со*. Асимптотическая ЛАЧХ (рис. 2.9, б) при о) < coi параллельна оси частот, а при О) coi имеет наклон - 40 дБ/дек.

Следует иметь в виду, что асимптотическая ЛАЧХ (рис. 2.9, б) при малых значениях коэффициента демпфирования довольно сильно отличается от точной ЛАЧХ. Точную ЛАЧХ можно построить по асимптотической ЛАЧХ, воспользовавшись кривыми отклонений точных ЛАЧХ от асимптотических (рис. 2.9, г).

Решив дифференциальное уравнение (2.49) колебательного звена при ы = 1 (/) и нулевых начальных условиях [у (0) =

= у (0) = 01, найдем переходную функцию:

h {t) = k==

е- sin(p-f Фо)

где a = i/T; p = kl Весовая функция

-i/T; q)o = arctg-

sinp/.

По переходной характеристике (рис. 2.9, в) можно определить параметры колебательного звена следующим образом.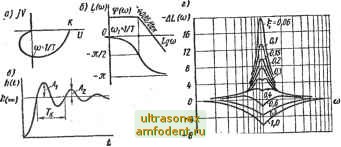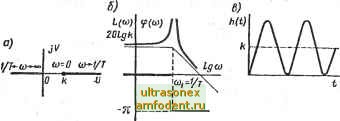

Рис. 2.10

Передаточный коэффициент k определяют по установившемуся значению h (оо) переходной функции. Постоянную вре-мении Т и коэффициент демпфирования можно найти из. уравнений

2п; ЛМ2 = е н

.p=-2n/T ;a=J-ln.

гт Тк - период колебаний; и Ла - амплитуды двух соседних колебаний относительно установившегося значения (рис. 2.9, е).

Консервативное звено (g = 0). Передаточная функция

1Г (s) = A;/(TV + 1). Частотная передаточная функция

W Ци)) = k/(\ - Гю).

Фазовая частотная функция, как это следует из АФЧХ рис. 2.10, а),

О при (о<: 1/Т; -л при to > 1/Т

ф((0) =

Это выражение можно получить из фазовой частотной функции колебательного звена предельным переходом при S -> 0. Нетрудно выписать выражения для оста.льных частотных функций; ЛЧХ приведены на рис. 2.10, б. Переходная функция

А (О = А: (1 - cos coi t); = 1/Т

Переходная характеристика (рис. 2.10, в) представ.ляет собой график гармонических ко.лебаний.

Апериодическое звено второго порядка ( 1). Передаточную функцию (2.50) при I 1 можно преобразовать к виду

(T,s+\)(rs-\-l)

Апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка. Оно не относится к числу элементарных звеньев.

Форсирующее звено второго порядка. Так называют звено, которое описывается уравнением

y = k {TY + Шр + 1) м

или, что то же, передаточной функцией

W (s) = k (TV + 2lTs + 1) (2.52)

при условии, что о g < 1.

Не представляет трудности получить выражения для частотных и временнйх функций и построить соответствующие характеристики.

На рассмотрении этих вопросов останавливаться не будем, Заметим только, что при частотах, превышающих сопрягают щую частоту, ЛАЧХ имеет нак.лон 40 дБ/дек и ЛФЧХ получается зеркальным отражением относительно оси частот ЛФЧХ соответствующего колебательного или консервативного звена. Если I 1, то звено с передаточной функцией (2.52) не относится к числу элементарных; его можно представить как последовательное соединение двух форсирующих звеньев первого порядка.

Неминимально-фазовые звенья. Звено называют минимально-фазовым, если все нули и полюсы его передаточной функции имеют отрицательные или равные нулю вещественные части. Звено назьшают неминимально-фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.

Напомним, что нулями передаточной функции W (s) = = R (s)/Q (s), где R (s) и Q (s) - полиномы от s, называют кор-