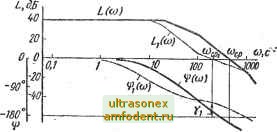Рис. 5.20

На рис. 5.20 показаны логарифмические частотные характеристики разомкнутой цепи исходной системы (сплошные линии) и системы с дополнительным звеном (пунктирные линии). В замкнутом состоянии система с дополнительным звеном устойчива, запас устойчивости по фазе = 49°.

Устойчивость достигнута смещением вниз среднечастоткой части ЛАЧХ, и данный прием называют демпфированием с подавлением средних частот. Этот вид демпфирования промежуточный между двумя первыми, и применяют его наиболее часто.

Рассмотренные приемы стабилизации и демпфирования систем автоматического регулирования являются основными, но далеко не исчерпывают всех возможностей.

§ 5.6. Выбор параметров и синтез корректирующих устройств по корневым годографам

Наглядность и простота исследования влияния отдельных параметров системы на ее динамические свойства составляют несомненные достоинства метода корневых годографов и обусловливают его применение как для выбора параметров, так и для синтеза корректирующих устройств.

Пусть требуется выбрать какой-то параметр а (передаточный коэффициент элемента, постоянную времени, коэффициент демпфирования). Тогда при постоянных значениях всех остальных параметров нужно задавать различные значения а ag, ... внутри возможных пределов изменения этого параметра

в данной системе и построить траектории корней (корневой годограф). Затем можно выбрать такое значение а, при котором имеет место наиболее благоприятное расположение нулей и полюсов. Корни следует вычислять наиболее простым чис- ленным методом, так как большой точности не требуется из-за приближенности корневой оценки качества.

Для выбора значения передаточного коэффициента k разомкнутой системы необходимо построить корневой годограф при изменении k. Способ построения такого корневого годографа разработан весьма детально (см. § 4.6).

При синтезе корректирующего устройства используют различные исходные положения. В простейшем случае полагают, что переходный процесс зависит от ближайшего к мнимой оси вещественного полюса. Вместе с тем пользуются и предположением, что наилучшие динаглические свойства система имеет, когда ближайшей к мнимой оси будет пара комплексно-сопряженных полюсов. Однако добавление третьего ближайшего к мнимой оси вещественного полюса обычно улучшает качество переходного процесса.

Необходимо также учитывать влияние нулей передаточной функции, поэтому для определения качества переходного процесса наиболее правильно рассматривать три ближайших полюса и один нуль передаточной функции замкнутой системы.

Порядок синтеза также может быть различным. Пусть требуется выбратё последовательное корректирующее устройство по заданным показателям качества переходной характеристики и при заданном значении передаточного коэффициента k разомкнутой системы. Тогда можно поступать следующим образом [И: выяснить влияние k на показатели качества; построить корневой годограф нескорректированной системы при изменении k и отыскать на нем точки, соответствующие заданным показателям качества; добиться прохождения траекторий корней при заданном значении k вблизи выбранных точек, вводя дополнительные нули и полюсы; составить передаточную функцию последовательного корректирующего устройства по дополнительно введенным нулям и полюсам.

Следует иметь в виду, что при введении диполя, т. е. полюса и нуля, близко расположенных друг к другу, показатели качества почти не изменяются, но передаточный коэффициент может быть увеличен.

Пример расчета по изложенной схеме приведен в [1].

Предположим, что динамика системы определяется парой комплексно-сопряженных полюсов;

%,02 = - о ± / о- (5.34)

Тогда передаточная функция замкнутой системы

W (s) =- kgl(Tl + 2Го io s + 1).. (5.35)

Ha основании переходной характеристики, соответствующей этой передаточной функции, определяют зависимость а и (Оо от времени регулирования /р и относительно перерегули-рования а [31, т. е.

оЗДр-, а = е- / . (5.36)

Теперь синтез последовательного корректирующего устройства по заданным значениям k, н а будет слагаться из следующих этапов:

1. Намечают положение определяющей пары полюсов Sqi и So2, т. е. пары полюсов передаточной функции (5.35), которая приблизительно эквивалентна передаточной функции скорректированной системы на основаницаданных показателей качества /р и а. При этом используют соотношения (5.36). На диаграмме достаточно отметить только один полюс sx-

2. Наносят на диаграмму полюсы и нули неизменяемой части системы.

3. Вводят дополнительные нули и полюсы так, чтобы траектория корней скорректированной системы при изменении k проходила вблизи полюса Sqi.Желательно скомпенсировать нулями ближайшие к мнимой оси полюсы неизменяемой части системы, с тем чтобы влияние полюсов s и s на динамику системы было действительно определяющим. Точка Sq, будет принадлежать траектории корней скорректированной системы, если удовлетворяется уравнение фаз (4.36).

4. Вводят диполь так, чтобы передаточный коэффициент k имел необходимое значение. При этоМ для вычисления k используют (4.37).

5. Составляют передаточную функцию последовательного корректирующего устройства по введенным полюсам и нулям.

6. Для проверки выполнения требований строят переходную характеристику скорректированной системы.

Пример 5.1. Передаточная функция неизменяемой части системы

Н/о (S) = kl[s (0,ls+ I) (0,05s Ч- 1)].

Требуется выбрать последовательное корректирующее устройство, обеспечивающее при 10 следующие показатели качества: 0,5 с