Получим дифференциальное уравнение системы, рассмотренной в примере 2.4 (рис. 2.22, а). Для нее

У = Wygg + W . (2.53)

Это дифференциальное уравнение в символической форме, связывающее выходную величину у с входными величинами. Аналогично можно записать дифференциальное уравнение относительно любой другой выходной величины. Исходя из определения передаточной функции нетрудно перейти от урав нения (2.53) к обычной несимволической форме записи.

Допустим, например, что Wi = ft,; Wi = kJ{p + 1); = kjp; = K. Тогда

где k = l/ikks); n = Vk; = (1 + kk - A) /{к кз);

Поэтому на основании (2.53)

ПуТу I-y-=Tsg + g + k(f + f).

Частотные характеристики. При исследовании и проектировании автоматических систем обычно используют амплитудно-фазовые и логарифмические частотные характеристики разомкнутых систем. Передаточные функции W (s) разомкнутых одноконтурных, а иногда и многоконтурных систем можно преобразовать к виду

№(s)= ri Wiis), (2.54)

где Wj (s) - передаточные функции элементарных звеньев.

В этом случае модули и аргументы частотных передаточных функций системы и звеньев А (ю) = \W (/ю)!; Ai {(,)) = \Wi ф ((о) = argU/(/со); фг (со) = arg Wi(j(a)

в соответствии с правилом модулей и аргументов комплекс ных чисел связаны между собой соотношениями

Л(со)= П Л,( ); (2.55)

Ф((й) -= 2 Фг( )- (2-56)

Вещественные и мнимые частотные функции системы определяются равенствами

и (со) = А (со) cos ф (со);

У (со) =Л(со) sin ф (со).

Пользуясь полученными соотношениями можно построить АФЧХ. Из (2.55) очевидно

L(co)- 2 L,(co).

(2.55)-

(2.57) (2.57),

(2.58)

где L (со) = 20 Ig А (со) и U (со) = 20 Ig Аг (со) - логарифмические амплитудные частотные функции.

Из (2.56) и (2.58) вытекает следующее правило построения ЛЧХ (ЛАЧХ и ЛФЧХ) систем, передаточные функции которых преобразованы к виду (2.54): строят ЛЧХ отдельных звеньев и затем их графически складывают.

На основании (2.58) можно также сформулировать несколько иной, более простой порядок построения ЛАЧХ. Проиллюстрируем это сначала на конкретном примере.

Пусть W (s)=100 (s4-l)/Is X X (10s-Ь 1) (0,01 £2 -f0,Is+l)].

Логарифмическая амплитудная частотная функция L(<u) = 40-v201g<й- -20 lgl/(10co)2+ 1 + -f20 Ig/ f72lj7i

-20 Ig 1/(1 -0,010)2)2-1.(0,1(0)2. Асимптотическая ЛАЧХ рассматриваемой системы состоит из четырех асимптот (рис. 2.28, а, б, в) и строится следующим образом. Вычислим сопрягающие частоты:

щ = 1/10 = 0,1; 2 = 1;

Здесь

= 1/0.1 = 10.

Щ, 2 и 0)д

сопрягаю-

щие частоты апериодического, форсирующего и колебательного звеньев соответственно.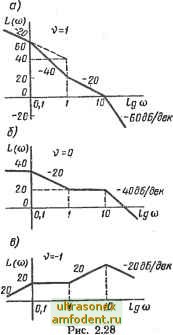

Напомним, что при построении асимптотической ЛАЧХ элементарных звеньев при частотах, меньших сопрягающей частоты, под корнем оставляют только единицу (остальными членами пренебрегают), а при частотах, больших сопрягающей частоты, -члены с наивысшей степенью со. Поэтому в рас--сматриваемом примере при со < coi

L (со) 40 - v20igco.

Это уравнение первой асимптоты. Согласно этому уравнению, первую асимптоту проводят через точку с координатами сй = 1 и L =.20 ig й с наклоном - v20 дБ/дек. Она кончается на первой сопрягающей частоте.

При сй1 о) <: аналогично имеем

L (со) ж 40 - v201g со - 20ig Юсо = 20 - v 20 Igco - - 20 Igco.

Это- уравнение второй асимптоты. Ее наклон изменяется на - 20 дБ/дек и обусловливается апериодическим звеном. Вторую асимптоту проводят от конца первой асимптоты до второй сопрягающей частоты согласно ее уравнению с наклоном (- V 20-20) дБ/дек.

При сй2 Сй < COg

L (со) ft( 20 - v201gco - 201go) 20igco = 20 - vx X20 Igco.

Это уравнение третьей асимптоты. Ее наклон изменяется на 20 дБ/дек и обусловливается форсирующим звеном. Третью асимптоту проводят от конца второй асимптоты до третьей сопрягающей частоты с наклоном - v-20 дБ/дек.

При со > со3 .

L (со) = 20 - v-20lgco - 40 ig 0,1 со = 60 - v201gco - - 401g CO.

Это уравнение последней, четвертой, асимптоты. Ее наклон изменяется по отношению к третьей асимптоты на -40 дБ/дек и обусловливается колебательным звеном.

Теперь нетрудно сформулировать общее правило построения асимптотической ЛАЧХ системы с передаточной функцией вида

W{s) П U7,(s), где Wi (s) - передаточные функции элементарных звеньев.