/21 = Пес\(0 + т!ё=в(0]й;

(4.58)

= ( [е!в (О -!- т? ё=о (О -I- - + <> (01 dt, (4.59)

где Ti, Та, т - постоянные величины.

Оценки /21,/2г называют обобщенными квадратичными оценками.

Геометрический смысл интегральной квадратичной оценки пояснен на рис. 4.21. Выбирая параметры системы по минимуму квадратичной интегральной оценки J20. приближаем кривую (О к осям и t.

Методы вычисления этих оценок предложены А. И. Мандельштамом й Н. Д. Папалекси в 1909 г. В 1937 г. акад. А. А. Харкевич применил эту оценку для исследования режимов работы усилителей, в 1948 г. А, А. Красовский и А. А. Фельд-баум использовали ее для исследования качества линейных систем автоматического регулирования.

Рассмотрим методы вычисления квадратичных интегральных оценок (О == JycT - h (t). По определению,

L{A(0}-(s) = -Lu7g,(s).

По теореме о предельных переходах.

= lim h (t) = lira sH (s) W. (0);

следовательно.

oB(s) = U7g (0)-U7g,(s).

Поскольку (s) - дробно-рациональная функция, то и И (s) можно записать в виде дробно-рациональной функции:

Я(5) =

aas +ai s -+ ... +а , sH-a

(4.60)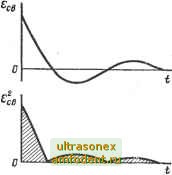

при m<Z п оценку J20 (4-57) можно вычислить, используя коэффициенты bo, b и Go, g (4.60), по формулам, приведенным ниже &з вывода [4]:

/20 = 1 ее (О dt = -- {Во\ + ByAy + ... + Д а +

+ В , Д , -Ь б Д) - , (4.61)

где Д - определитель Гурвица, составленный из коэффициентов:

(4.62)

в котором все коэффициенты с меньшим индексом О и большим п заменяют нулями. Определители До, Д получают из (4.62) заменой столбца (v + 1) столбцом a i, а 0, .... О, а V = О, 1, .... т.

Коэффициенты Во. В, В-ъ В определяют как

Bo = bfn; Bybl i-2bbrn-2,

Bv-b v-2bm v+!bm-v-l Н- ... + 2{--lrbbm-2v;

(4.63)

Интегральную квадратичную оценку /20 можно вычислять по заданной частотной характеристике замкнутой системы.

Пусть Е (/со) - изображение Фурье для функции бсв (0. на основании теоремы свертки в комплексной области для Е {бсв (О бсв (0} можно записать [7] при s = О

оо оо

Ло = J (О = f I со (р) Г (4.64)

есв (О = Луот- л (О Ф со (/ ) = 4- [ycoWgh (0) - (/ )].

(4.65)

где Wgii (/lo) - комплексный коэффициент усиления замкнутой системы.

Таким образом, по (4.64) и (4.65) можно вычислить Jo. Выражение (4.64) есть формула Рэлея*.

Существуют таблицы расчета интеграла /о в функции коэффициентов bo, bri: и щ, an изображения по Лапласу сигнала ошибки £св (s) для т = п - 1 и до п = 10. В табл. 4.1 приведены формулы для Jo при == 1 -f- 5.

,: . . Таблица 4.1

bps + by / - + +Ьт-1 S +Ь,п

Есв (S) =-----;--

aos +ais + ...-fa ,s+an n=l. /2o=6g/(2aoai). n = 2. /20 = (frf ao + frao2)/(2aoci 2). , fcg as Oj + (bi -2Ьо ba) ао i о

fc§ (-а 14- Ui as oa) -f- (6 -22 6o) 4 s o -b n=4 / + (bj -2Ьз fri) До + bj (- ЯзЯр + 2 Я1 Ор) . °° 2а4ао(-a4 i-ОзЯс+Охагйз)

= 5. /,0= 7[fcgmo4-(Ь?-2fc2bo) l4-6i-26зfc,--

2A5L

+ 24 6о)п2 + (* - 264 62) 3 4- bl 4

0 = -{агЩ-ац,т\) т=~ {am-axtni); ао од

1=-йб 0:2 + 0403; 4 = --(йзИз-схз);

2=-05 00 + 04 cj; Ао = 05(й4т4-02mз--aon2)

Пpи выборе параметров системы по минимуму оценки /go часто получают нежелательную колебательность процесса, так как приближение процесса h (t) к идеальному скачку вызывает резкое увеличение начальной скорости, что, в свою очередь, может вызвать высокое перерегулирование, умень-

* Эта формула была получена и Парсевалем, поэтому в литературе ее также называют и формулой Парсеваля.