нения были левыми; иначе говоря, среди них не должно быть корней, лежащих на мнимой оси и обращающих в нуль комплексный прлином D (/о), т. е. должно выполняться еще одно условие

В{1<л)фО. (3.61)

Формулы (3.60) и (3.6!) представляют математическое выражение критерия устойчивости Михайлова: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы вектор кривой Михайлова D (/ю) при изменении а от О до оо повернулся, нигде не обращаясь в нуль, вокруг начала координат против часовой стрелки на. угол пп12, где п - порядок характеристического уравнения.

Заметим, что для усгойчивых систем кривая Михайлова начинается при <в = О на вещественной положительной полуоси, поскольку при Go > О все коэффициенты характеристического уравнения положительны и Оф) = > 0. Кроме того, для устойчивых систем, описываемых обыкнЬвенными дифференциальными уравнениями с постоянными коэффициентами, фаза (аргумент) яр (ю) с ростом частоты ю должна возрастать монотонно, т. е вектор D (/<о) должен поворачиваться только против часовой стрелки, поскольку с ростом частоты монотонно возрастают имеющие одинаковые (положительные) знаки фазы элементарных векторов (/ю s), являющиеся слагаемыми фазы вектора D(/o)) (см. (3.53)).

Учитывая сказанное выше, критерий устойчивости Михайлова можно сформулировать так: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты со от О до оо, начинаясь при (о - О на вещественной положительной полуоси, обходила только против часовой стрелки последовательно п квадрантов координатной плоскости, где п - порядок характеристического уравнения.

Кривая Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического уравнения.

На рис. 3.9 показаны типичные кривые Михайлова для усгойчивых систем, описываемых уравнениями, начиная от первого (п = 1) и кончая пятым (п = 5) порядком. Для удобства сравнения коэффициенты во всех случаях приняты одинаковыми.

Признаком неустойчивоеги систерлы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора D (/со) оказывается меньше, черл я/г/2. Число правых корней неустойчивой системы можно определить по (3.59).

На рис. 3.10 показаны кривые Михайлова для неустойчивых и нейтральных систем. Рис. 3. Ю, а - при ю = О кривая Михайлова начинается на отрицательной вещесгвенной полуоси; система неустойчива. Рис. 3.10, б - порядок уравнения n = 5, а кривая Михайлова находится вся в одном квадранте (этому соответствует характеристическое уравнение D (s)= = GeS* + GiS* + Gg = 0); система неустойчива. Рис. 3.10, в - нарушена последовательность прохождения квадрантов; система неустойчива. Рис. 3.10, г-кривая Михайлова начинаег-ся в начале координат, т. е. в характеристическом уравнении имеется по крайней мере один нулевой корень; система находится на границе апериодической устойчивости; небольшая деформация кривой Михайлова (прерывистая линия) делает систему устойчивой. Рис. 3.10, д - кривая Михайлова йроходит при некотором значении частоты Юк через начало координат, т. е. в характеристическом уравнении имеются чисто мнимые корни ± /<Ва; система находится на границе колебательной устойчивости; небольшая деформация кривой Михайлова делает систему устойчивой (прерывистая линия). Рис. 3.10, е - кривая Михайлова проходит через начало координат, но небольшой деформацией кривой Михайлова удовлетворить условиям устойчивоеги нельзя; систерля неустойчива.

Поегроение кривой Михайлова практически производится либо методом контрольных точек, либо методом вспомогательных годографов. Первый метод сводится к определению ряда точек кривой Михайлова, соответствующих фиксированным значениям частоты О), включая (обязательно) часготы точек пересечения кривой с осями координат, которые находятся как корни уравнений (3.62) и (3.63). При втором методе предварительно определяют годографы отдельных звеньев си-Рис. 3.9 стемы и по ним строят искомую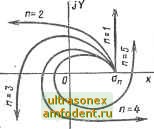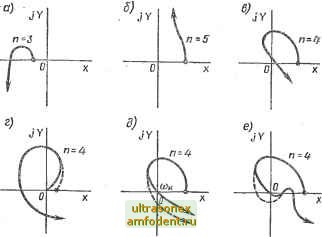

Рис. 3.10

кривую Михайлова, применяя правила умножения и сложения векторов.

Анализируя годографы Михайлова, можно установить следующее следствие из критерия устойчивости Михайлова. При последовательном рохождении кривой Михайлова квадрантов координатной плоскоеги вещественная и мнимая оси пересекаются ею поочередно. В точках пересечения кривой Михайлова с вещесгвенной осью обращается в нуль мнимая функция Михайлова Y (ю), а в точках пересечения кривой с мнимой осью обращается в нуль вещественная функция X (ш). Поэтому - значения частот, при которых происходит пересечение кривой с вещественной или мнимой осью, должны являться корнями уравнений

X (о) = 0; (3.62)

К (ю) = 0.

(3.63)

Вещественную X (ю) и мнимую Y (ю) функции Михайлова можно представить графически в виде кривых (рис. З.П). Точки пересечения этих кривых с осью абсцисс дают значения корней уравнений (3.62) и (3.63). Если значения о, т, (Hi, ... есть корни уравнения (3.63), а о)1,;о)з,;со5- уравнения (3.62), причем о <а < < 4 <-мЮ1 < < coj....