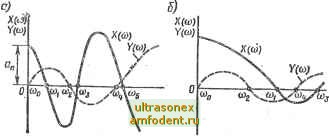Рис. 3.11

то для устойчивой системы обязательно соблюдение неравенства

о < i< 0)2 < 0)3 < 0)4 < 0) < ... . (3.64)

В связи с указанным следствием можно привести другую формулировку критерия устойчивости Михайлова: система, автоматического управления будет устойчива тогда и только тогда, когда вещественная X (со) и мнимая Y (ю) функции Михайлова, приравненные нулю, имеют все действительные и перемежающиеся корни, причем общее число этих корней равно порядку характеристического уравнения п, и при ю = О удовлетворяются условия

X (0) > О, У (0) > 0.

На рис. 3.11, а приведен пример графиков X (ю) и У (со) для устойчивой системы, а на рис. 3.11,6 - для неустойчивой системы.

Для уравнений до шестого по{)ядка включительно условие перемежаеглости корней дает возможность легко провести аналитическое исследование устойчивости, не вычерчивая кривую Михайлова. При этом обычно определяют только корни уравнения У (со) = 0. Перемежаемость корней уравнений X (со)=0 и F (со) = О можно проверить подстановкой в X (со) найденных корней уравнения У (со) = 0. Как видно из рис. 3.11 ,а, знаки X (со) при подстановке возрастающих по абсолютной величине корней должны чередоваться.

Пример 3.6. Определить устойчивость системы, характеристическое уравнение которой

D (S) = se -f 6s5 -f 15s + 20 il5s+6s + 1 = 0.

Подставляем s = /со и находим вещественную и мнимую функции Михайлова:

X (й>) = -о) + 15&)4 - 15&)2 +1 = 0;

К (со) = со (6w* - 200)2 + 6) = 0.

Находим корни уравнений V (сй) = О, т. е. Wo = 0; СО4 - З.ЗЗм* + -j- 1 = О, откуда

1.4= 1.67 гЬ 1/2,78-1; w=0,36; со=2,%.

Если перемежаются корни, то перемножаются и их квадраты, поэтому нахождение cOg и со не обязательно.

Проверим, чередуются ли знаки X (со) при подстановке (в и о>. Имеем

X fcoj = -0,36 + 15-0,36 - 15-0,36 + 1 - -2,51;

X (щ) = -2,96 + 15-2,96 - 15-2,96 + 1 > 0.

Так как все корни К (ев) вещественны и знаки ординат X (со), соответствующие этим корням, чередуются, то система устойчива.

Критерий устойчивости Найквиста. Этот частотный критерий устойчивости, разработанный в 1932 г. американским ученым Г. Найквистом, позволяет судить об усгойчивости замкнутой системы по виду амплитудно-фазовой характеристики разомкнутой системы.

Пусть передаточная функция разомкнутой системы

W(s)Л=..Ьl±h£!- + +r тп. (3.65)

Подставляя в (3.65) s = /со, получаем частотную передаточную функцию разомкнутой системы:

IF (/со) г-.- ° </й>) + h -Ь + V

Q (/ ) Со (/й>) 4- сг Uayf- Ч ... + с

= £/ ((0) -f jV (со) = А ((й) еШ), (3.66)

где (7 (со) и Y (со) - действительная и мнимая части частотной передаточной функции соотвегственно; модуль А (со) и фаза яр (со) частотной передаточной функции равны А (со) =

= (Сй) -t- V (со); яр (со) = Arctg

Если изменять частоту со от -с до оо, то вектор W (/со) будет меняться по величине и фазе. Кривую, описываемую концом этого вектора в комплексной плоскости, называют ампли-

VJUio)

и (О))

тудно-фазовой характеристикой разомкнутой системы (рис. 3.12).

Амплитудно-фазовая характеристика симметрична относительно вещественной оси, поэтому обычно вычерчивакуг только ту часть ее, которая соответствует положительным частотам о)>0 (сплошная линия на рис. 3.12), а ветвь этой характеристики, соответствующая отрицательным частотам ю < О (пунктирная линия на рис. 3.12), может быть найдена как зеркальное отражение ветви, соответствующей положительным частотам, относительно вещественной оси. Рассмотрим вспомогательную функцию

is)=l + W(s)=l+R {s)/Q is) = IQ is) + R is)]/

/Q is), = D is)/Q is), (3.67)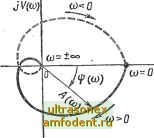

Рис. 3.12

+ an - Q{s) = полином

+ 6m-

где D is) = Q is) + R (s) = о + OiS + характеристический полином, замкнутой систерлы;

- CoS + CiS - + ... -f c - характеристический разомкнутой системы; R (s) = bo, s + bys - + ..

- полином степени т.

Заметим, что так как в реальных системах степень полино-рла R is) не выше степени полинома Q (s), т. е. m п, то степени числителя и знаменателя дроби (3.67) одинаковы и равны п.

Подставляя в (3.67) s = /ю, получирл

Ф (/(о) = 1 -f Г (/(о) = [Q (/o>)-f i?(/o>)]/Q(/co) = D (/<B)/Q (/со).

(3.68)

Пусть характеристическое уравнение замкнутой системы D (5) = О имеет т правых корней и п-т левых корней, а характеристическое уравнение разомкнутой системы Q (s) == О имеет I правых и п - / левых корней.

При изменении частоты со от - оо до оо изменение угла поворота вектора р (/со) на основе принципа аргумента будет

AArgq (/со) = я[(п-

:!1со = А Arg D (/СО) -Л ArgQ (/со) = т) -т] -я 1(п -/)-Л = 2л (I -т). (3.69)