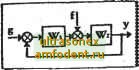МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ

§ 2.1. Уравнения динамики и статики. Линеаризация

На определенном этапе разработки и исследования автоматической системы управления получают ее математическое описание - описание процессов, проистекающих в системе, на языке математики. Математическое описание может быть аналитическим (с помощью уравнений), графическим (с помощью графиков, структурных схем и графов) и табличным (с помощью таблиц).

Для получения математического описания системы обычно составляют описание ее отдельных элементов. В частности, для получения уравнений системы составляют уравнения для каждого входящего в нее элемента. Совокупность всех уравнений элементов и дает уравнения системы.

Уравнения (а также структурные схемы) автоматической системы управления называют ее математической моделью. Такое название обусловлено тем, что при математическом описании (составлении уравнений) физических процессов всегда делают какие-либо допущения и приближения. Математическая модель одной и той же системы в зависимости от цели исследования может быть разной. Более того, иногда полезно при решении одной и той же задачи на разных этапах принимать разную математическую модель: начать исследование с простейшей модели, а затем ее по-

степенно усложнять, с тем чтобы учесть дополнительные явления и связи, кото-У рые на начальном этапе были отброшены как несущественные. Сказанное обусловливается тем, что к математической модели предъявляются противоречивые тре-Рис. 2.1 бования: она должна, с одной стороны,

как можно полнее отражать свойства оригинала, а с другой стороны, быть по возможности простой, чтобы не усложнять исследование.

Система управления и любой ее элемент производят преобразование входного сигнала х {t) в выходной сигнал у (0. С математической точки зрения они осуществляют отображение

у (t) = Ах (t),

согласно которому каждому элементу х (i) из множества X входных сигналов (х (/) £ X) ставится в соответствие единственный, вполне определенный элемент у (f) из множества Y выходных сигналов 1у (t) g Yl. В приведенном соотношении А называется оператором. Оператор, определяющий соответствие между входным и выходным сигналами системы управления (элемента), называется оператором этой системы (элемента). Задать оператор системы - это значит задать правило определения выходного сигнала этой системы по ее входному сигналу.

Рассмотрим математическое описание непрерывных систем управления с помощью дифференциальных уравнений. В большинстве случаев звенья и системы описываются нелинейными дифференциальными уравнениями произвольного порядка. Здесь под звеном понимается математическая модель элемента. Для примера рассмотрим звено (рис. 2.1), которое можно описать дифференциальным уравнением второго порядка

Fiy,y,y,u,d) + fO. (2.1)

где у - выходная величина; ы и / - входные величины; у

к и - первые производные по времени; у - вторая производная по времени.

Уравнение (2.1), описывающее процессы в звене при произвольных входных воздействиях, называют уравнением динамики. Пусть при постоянных входных величинах и = u9 и / = /< процесс в звене с течением времени установится:

выходная величина примет постоянное значение у Тог-

да (2.1) примет вид

= (уО,0,0.ио,0)+ = 0. (2.2)

Это уравнение описывает статический или установившийся режим и его называют уравнением статики.

Статический режим можно описать графически с помощью статических Характеристик. Статической характеристикой звена или элемента (а также системы) называют зависимость выходной величины от входной в статическом режиме. Статическую характеристику можно построить экспериментально, подавая на вход Элемента постоянное воздействие и измеряя выходную величину после окончания переходного процесса, или расчетным путем, используя уравнение статики.

Если звено,имеет несколько входов, то оно описывается с помощью семейства или семейств статических характеристик. Например, звено, характеризукщееся в статическом режиме уравнением (2.2), можно описать графически с помощью семейства статических характеристик, представляющих собой кривые зависимости выходной величины у от одной входной величины и (или /) при различных фиксированных значениях другой - / (или и).

Линеаризация. Обычно автоматические системы описывают нелинейными дифференциальными уравнениями. Но во многих случаях можно их линеаризовать, т. е. заменить исходные нелинейные уравнения линейными, приближенно описывающими процессы в системе. Процесс преобразования нелинейных уравнении в линейные называют линеаризацией.

В атоматических системах должен поддерживаться некоторый заданный режим. При этом режиме входные и выходные величины звеньев системы изменяются по определенному закону. В частности, в системах стабилизации они принимают определенные постоянные значения. Но из-за различных возмущающих факторов фактический режим отличается от требуемого (заданного), поэтому текущие значения входных и выходных величин не равны значениям, соответствукщим заданному режиму. В нормально функционирующей автоматической системе фактический режим немного отличается от требуемого режима и отклонения входных и выходных величин входящих в нее звеньев от требуемых значений малы. Это позволяет произвести линеаризацию, разлагая нелинейные функции, входящие в уравнения, в ряд Тейлора. Линеаризацию можно производить по звеньям.