выбираем вектор строку р = (0,6; 0,1; 0,3). Исходящей ЛС первого выбора является ЛС к УК № 1. Предположим, что данная ЛС в настоящий момент времени недоступна. Так как pj > pJ, то исходящей ЛС второго выбора является ЛС к УК № 4. Допустим, что исходящая ЛС из УК № 2 к УК № 4 в данный момент времени доступна. Следовательно, данная ЛС участвуете организации искомого маршрута. В УК № 4 в соответствии с Р/ = (0,7; 0,2; 0,1) выбираем исходящую ЛС к УК № 1. Допустим, она доступна. Следовательно, маршрут между УИ и УП i2,i = {2, 4, 1} организован. ЛС, участвующие в данной процедуре, поощряются. Соответствующие весовые коэффи-циенты р{, р\> увеличиваются (предположим, что на 0,2), а вектора Р/\ Р/* нормируются. В результате получаем новые числовые значения: Р/г> = (0,5; 0,08; 0,42); Р/ = (0,75; 0,17; 0,08).

Если ситуация поиска маршрута между заданной парой УК повторится, то вектора Р/ Р/ изменятся и примут следующий вид: р;2) = (0,42; 0.07: 0.51): Р/ = (0,79; 0,14; 0,07). Анализируя ситуацию с вектором Р/2, видно, что исходящая ЛС к УК № 4 из УК № 2 при поиске маршрута к УК № 1 приняла значение первого выбора, так как ее весовой коэффициент р\ стал максимальным из всех возможных в данном векторе.

Матрицы весовых коэффициентов УК № 2 и 4 примут следующий вид:

р(2)

1 3 4

0,42 0,07 0,51

0,2 0,6 0,2

0,2 0,2 0,6

; Р* =

1 2 3

0,79 0,14 0,07

0,2 0,6 0,2

0,1 0,2 0,7

Если рассматривать весовые коэффициенты р)1> как вероятности выбора соответствующих исходящих ЛС m*j\ то можно предположить, что игровой метод решает задачу глобальной оптимизации сети связи по критерию - вероятность установления соединения между парами УИ и УП.

Отсутствие необходимости передачи служебной информации при формировании ПРИ на сети является несомненным достоинством ифового метода. Однако данный метод обладает инерционностью. Действительно, при выходе элементов сети связи из строя потребуется некоторый период времени для переформирования ПРИ на сети.

Логический метод [17] состоит в процедуре, выполняемой в каждом транзитном УК, начиная от УИ, позволяющей определить исходящую ЛС, максимально близкой к геометрическому направлению на УП.

Сеть связи вкладывается в прямоугольную систему координат. Каждому узлу сети присваивается собственный адрес {X, Y) (рис. 9.20).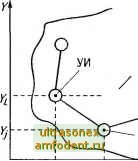

Сеть связи

Направление логического поиска

Транзитный узел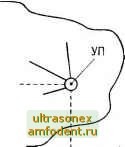

Рис. 9.20. Поиск маршрута логическим методом

В каждом транзитном УК {Х У,), начиная с УИ (Хя, Vl). производится анализ адреса УП сопоставлением его с собственным. В результате вычисляется геометрическое направление из данного узла на УП. Затем определяется та ЛС, которая имеет наибольшее совпадение с ранее рассчитанным геометрическим направлением на УП. Если ближайшая по направлению исходящая ЛС не доступна, то подбирается очередная по предпочтительности исходящая ЛС. Пример 9.7.

На рис. 9.21 представлена сеть связи, в которой УИ и УП, соответственно, имеют координаты {1, 2} и {10, 2}. Из УИ определяем геометрическое направление на УП (указано пунктиром). С данным направлением совпадает исходящая ЛС к узлу с координатами {4, 2}. В УК {4, 2} выбираем исходящую ЛС к УК с координатами {7, 3}, так как она имеет наименьший угол отклонения от геометрического направления

@{8,4} УП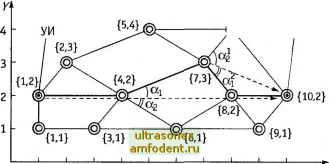

0123456789 10 X Рис. 9.21. Пример формирования ПРИ логическим методом

на УП. В УК {7, 3} подобным образом выбираем ЛС к УК {8, 2}. В УК {8, 2} выбираем ЛС к УК {10, 2}.

Таким образом: ц({1, 2}; {10, 2}) = ({1,2}, {4, 2}, {7, 3}, {8, 2}, {10, 2}). Достоинством данного метода является простота и отсутствие необходимости передачи служебной информации по сети. В то же время логический метод не является динамическим и не решает задачу глобальной оптимизации ПРИ.

Логически-игровой метод [17] формирования ПРИ является обобщением логического и игрового методов. По аналогии с логическим методом сеть связи вкладывается в прямоугольную систему координат, в соответствии с которой каждому узлу сети присваивается собственный адрес {X, У). В каждом УК у имеется матрица

P=p°tsO( .3);i = 1.W/;.y = 1.S;/Vy, которая имеет следующий вид:

И содержит S° строк. Учитывая, что возможно увеличение числа УК на сети, то S° выбирают таким, чтобы S° > S. Количество столбцов матрицы Р° для УК под номером у равно: (Ну + 3), где Ну - число исходящих ЛС из у-го узла; три столбца отводится для номеров УП, представленных в общепризнанной нумерации и прямоугольной системе координат (X, Y).

На момент ввода узла в эксплуатацию матрица содержит только информацию о смежных номерах УК с данными выраженных в прямоугольной системе координат: {Xqj, Yqj).....[Xvj, Vvy)> - , [Xhj, VWy). По

мере функционирования сети связи матрица Р° заполняется и корректируется.