v(t) = V{\ + McosQ.t)cos(ut. (2.2)

Параметр М, = AV/V называется глубиной амплитудной модуляции. При =0 модуляции нет и vit) = Voit), т.е. получаем не-модулированное несущее колебание (2.1). Обычно амплитуда несущего выбирается больше амплитуды первичного сигнала, так что

На рис. 2.3 показана форма передаваемого сигнала (а), несущего колебания до модуляции (б) и модулированного по амплитуде несущего колебания (в).

Произведя в (2.2) перемножение, получим, что амплитудно-моду-лированное колебание

(f) = V cos wf + (\ 2) cos (со + Q) f+

состоит из суммы трех гармонических составляющих с частотами со, co + Qhco-Qh амплитудами соответственно V, и .

Таким образом, спектр амплитудно-модулированного колебания (или АМ-колебания) состоит из частоты несущего колебания и двух боковых частот, симметричных относительно несущей, с одинаковыми амплитудами (рис. 2.4, б). Спектр первичного сигнала sit) приведен на рис. 2.4, а.

Если первичный сигнал сложный и его спектр ограничен частотами Qmin и Qmax (рис. 2.4, в), ТО спектр АМ-колебания будет состоять из несущего колебания и двух боковых полос, симметричных относительно несущей (рис. 2.4, г).

5(со)

5(со)

am 1/2

Ксо)

(o-Q со clH-Q

O-Qmax (O-Qmin Ы 0>+-Qn,ax CO+-Q ,ip СО Г

Рис. 2.4. Спектры синусоидального (а) и сложного (в) сигналов и модулированных ими по амплитуде несущих колебаний (б и г)

Анализ энергетических соотношений показывает, что основная мощность АМ-колебания заключена в несущем колебании, которое не содержит полезной информации. Нижняя и верхняя боковые полосы несут одинаковую информацию и имеют более низкую мощность.

2.3. Угловая модуляция

Можно изменять во времени пропорционально первичному сигналу sit) не амплитуду, а частоту несущего колебания:

сй( f) = со +/Сцм5( f) = со + Дсосоз Qf,

(2.3)

где /Сцм - коэффициент пропорциональности; величина Дсо = kS -называется девиацией частоты (фактически это максимальное откпо-нение частоты модулированного сигнала от частоты несущего колебания).

Такой вид модуляции называется частотной модуляцией. На рис. 2.5 показано изменение частоты несущего колебания при частотной модуляции.

При изменении фазы несущего колебания получим фазовую модуляцию

ф(?) = ф+/Сфм5(?) = ф+Дфсозй?,

(2.4)

где /Сф, - коэффициент пропорциональности; Дф = kS = Мф, - индекс фазовой модуляции.

Между частотной и фазовой модуляцией существует тесная связь. Представим несущее колебание в виде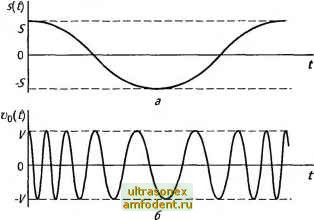

Рис. 2.5. Исходный (а) и частотно-модулированный (б) сигналы

2.3. Угловая модуляция 33

t)o(f) = Vcos(tof + 9) = Vcos4(f), (2.5)

где Ф - начальная фаза колебания, а 441) -evo полная фаза. Между фазой и частотой со существует связь:

4(t) = \(x)indt + (f). (2.6)

Подставим в (2.6) выражение (2.3) для co(f) при частотной модуляции:

4(f) = a)(0+(Aw/i2)sinQf.

Величина М ~ Aco/Q называется индексом частотной модуляции.

Частотно-модулированное колебание запишется в виде:

v(t) = Vcos{oit+Ms\nQt + (p). (2.7)

Фазо-модулированное колебание с учетом (2.4) для ф(?) следующее:

v(t)=Vcos{(x)t + McosQ.t+ (;>). (2.8)

Из сравнения (2.7) и (2.8) следует, что по внешнему виду сигнала vit) трудно различить, какая модуляция применена - частотная или фазовая. Часто оба эти вида модуляции называют угловой модуляцией, а М и Мф, - индексами угловой модуляции.

Несущее колебание, подвергнутое угловой модуляции (2.7) или (2.8), можно представить в виде суммы гармонических колебаний:

vU) = V{Io(M)cosoit+I,{M)cos{(u+Q)t + + /i(/W)cos(cu-Q)f + /2(/W)cos(cu + 2Q)f + + /2(/W)cos(cu-2Q)f + /3(/W)cos(cu+3Q)f + + /3(/W)cos(cu-3Q)f+ ...}.

Здесь М - индекс угловой модуляции, принимающий значение при ЧМ и Мф, при ФМ. Амплитуды гармоник в этом выражении определяются некоторыми коэффициентами /(/W), значения которых при различных аргументах приводятся в специальных справочных таблицах. Чем больше М, тем шире спектр модулированного колебания.

Таким образом, спектр модулированной несущей при угловой модуляции даже при гармоническом первичном сигнале sit) состоит из бесконечного числа дискретных составляющих, образующих нижнюю и верхнюю боковые полосы спектра, симметричные

2-3719