Механическая система

Iсистема аналогий

Электрическая модель

Жсистема аналогии

7 е Z

о-СП

о-ЬтЛ-о

о--1--о

о-(ет)-о

о---о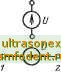

3 -о

7. -о

Схемы замещения элементов упругой системы при растяжении, составленные по методу электромеханических аналогий

Из четырехполюсников, замещающих отдельные элементы, составляется электрическая модель динамической системы в целом.

На рис. 6-2 приведен пример применения метода четырехполюсников к одномерной механической системе.

Модели многомерных систем составляются из многополюсников. Для задачи изгиба стержневых систем путь построения моделей заключается в том, что стержневая система моделируется по стержням - участкам системы. Каждый стержень замещается электрической схемой - восьмиполюсником, воспроизводящим связи между динамическими перемещениями, углами поворота, изгибающими моментами и перерезывающими силами на его концах. Участки стержневой системы соединяются между собой в соответствии с условиями сопряжения и граничными условиями.

Выше было показано, что для продольных и крутильных перемещений уравнения, связывающие значения сил и перемещений на концах каждого участка одномерной системы, выражаются так же, как и для электрических четырехполюсников. Задачи изгиба значительно сложнее, так как здесь необходимо для каждого участка воспроизвести в схеме замещения связи между восемью величинами.

Если представить участок стержневой системы в электрической модели в виде эквивалентного восьмиполюсника, то последний будет иметь четыре пары полюсов, на которых моделируются следующие механические величины:

f-W-1

-о-VW-

/77,

о--*-о-cvv-i-о-

Рис. 6-2. Механическая система и ее электрическая модель из пассивных четырехполюсников.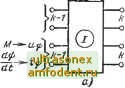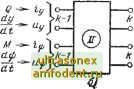

Рис. 6-3. Восьмиполюсники - модели участка стержневой системы по первой (/) и второй ( ) системам аналогий.

1) изгибающий момент Mh-i и угловое перемещение -фл-ь (угловая скорость ijjft-i) начала рассматриваемого участка;

2) перерезывающая сила Qh-i и прогиб yn-i (линейная скорость i/ft-i) начала рассматриваемого участка;

3) изгибающий момент и угловое перемещение фй (угловая. скорость ipfe) конца рассматриваемого участка;

4) перерезывающая сила Qh и прогиб уь (линейная скорость. yh) конца рассматриваемого участка.

По первой системе аналогий обобщенным силам на концах участка соответствуют напряжения, а обобщенным скоростям - ток (рис. 6-3,а), по второй системе аналогий обобщенным силам соответствуют токи, а скоростям--напряжения (рис. 6-3,6).

£3

L F=4 f

Рис. 6-4. Модель неразрезных балок с различными видами опор.

Общий метод построения электрических моделей для задач изгиба стержневых систем состоит в соединении восьмиполюсников, представляющих отдельные ее стержни, в соответствии с граничными условиями и условиями сопряжения. Граничные условия в моделях изгиба осуществляются так же, как и в моделях продольных и крутильных колебаний: жесткому закреплению по какой-либо координате в электрической модели по первой системе аналогий соответствуют разомкнутые полюсы, а по второй - полюсы, замкнутые-накоротко.

Из рис. 6-4 видны особенности электрического моделирования! неразрезных балок с различными видами опор.

Для упрощения чертежа здесь миогополюсиики упругих участков изображены в виде прямоугольников. Внутренние их схемы на> операционных усилителях рассматриваются далее.

6-2. модели прямой аналогии на операционных элементах

Желание сохранить преимущества физической наглядности метода прямой аналогии и вместе с тем ие прибегать к созданию специализированных установок, а использовать АВМ общего назначения, приводит к реализации моделей прямой аналогии на опера-