

 |
 |
|
Главная страница Схемы квантования Рассмотрим на примере мальтийского механизма применение указанной методики для моделирования двузначных циклических функций. На рис. 3-4,й изображена кривая изменения приведенного к валу кривошипа момента инерции J((f) для мальтийского механизма. Как следует из графика, приведенный момент инерции является циклической функцией угла поворота ф вала кривошипа с периодом 2я. В качестве аргумента используется периодическая функция sin ф (использование в качестве аргумента периодической функции cos ф нецелесообразно вследствие большой крутизны изменения преобразованной функции при cos ф->-!). На рис. 3-4,6 представ- лена зависимость приведенного момента инерции мальтийского механизма в функции sin ф вала кривошипа. Как видно из рисунка, приведенный момент инерции / при одних и тех же значениях аргу- Jfsin) о гг  Рис. 3-4. Нелинейные зависимости момента инерции мальтийского механизма / в функции ф и sin ф. мента sJn ф имеет два различных значения. Использование специальной релейной схемы, изображенной иа рис. 3-5, позволяет осуществить моделирование данной двузначной функции. Принцип работы схемы состоит в следующем. Нелинейная зависимость (sinф) набирается иа блоке нелинейности Ф, на выходе которого имеется контакт управляющего поляризованного реле Р1. На обмотку питания поляризованного реле подается SiPfP напряжение, пропорциональное cos ф. При положительных значениях напряжения, соответствующего cos ф (см. рис. 3-1,е), цепь замкиута на блок Ф и на выходе отрабатывается напряжение, соответствующее значению sin ф. При отрицательных значениях наиряжения, соответствующего со8ф, (sinф) = =const, т. е. не изменяется. Если при отрицательных значениях напряжения, соответствующего оо8ф, функция /(ф) переменна, то для отработки данной функции используется дополнительный блок нелинейности, а релейная схема осуществляет переключение с одного блока нелинейности на другой. Схемы электронного маятника находят в практике моделирования самые разнообразные применения, в частности, могут быть использованы для гармониче- о cosy Рис. 3-5. Схема моделирования характеристики, приведенной на рис. 3-4,6. ского анализа переменной. Схема электронного маятника постоянной частоты с дополнительным входом у интегрирующего усилителя и нулевыми начальными условиями на обоих интегрирующих усилителях моделирует поведение ЬС/?-фильтра при внешнем возмущении. При налич-ии в исследуемом сигнале гармоники, на которую настроена схема, происходит раскачивание выходного напряжения схемы до определенной амплитуды, характеризующей амплитуду данной гармонической составляющей в спектре исследуемого сигнала. Описанный способ характеризуется тем, что его приме-  Хгг -о
Рис. 3-6. Схема для реализации спирали Архимеда. Рис. 3-7. График спирали Архимеда. пение занимает много времени, а добротность такого фильтра должна быть небольшой, так как в противном случае процесс установления растягивается во времени. Схема связанных между собой двух электронных маятников (рис. 3-6) дает возможность получить спираль Архимеда на экране осциллографа (рис. 3-7): где Го - радиус второго витка спирали. Для данной схемы имеем: л;21=Гоют sin ют; л:22=/оит cos ©т; График на фазовой плоскости получается при включении сигналов л;21 и Х22 соответственно на вертикальный и горизонтальный входы осциллографа. Ниже приведены некоторые примеры схем генерирования различных функций. 3-2. схемы генераторов некоторых единичных сигналов в функции времени 3-2-1. Схема, воспроизводящая линейно-возрастающую функцию с ограничением. 
Параметры схемы связаны с графиком соотношениями: tgф==(Л-ЬB)/Ti=ai; а2=Л/(1-ЬЛ) и аз==В. Здесь и далее Л и В представлены в относительных единицах (к шкале 100 В). значения ограничения в за- висимости от характеристики диода. Погрешность работы схемы зависит от уровня ограничения Л. 3-2-2. Схема генератора единичных сигналов. 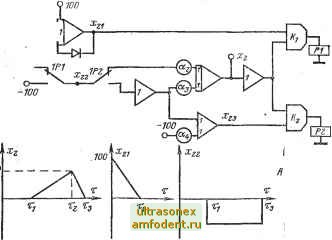
|
|||||||||||||||||||||||||||||
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |