Производные этой функции; z=b-{-2ct-l-3dfi; z =2c-\-Mt; z = &d.

При Za-a, za=b и z o=2c, определяющее уравнение z =6d. - 5. Получить определяющее уравнение для функции z=l/(e-)-

Так как z==-b/(a-\-bt)\ то при Zo=l/a определяющее уравнение имеет вид z-{-bz=0.

Часто при исследовании динамики различных систем возникает необходимость создайия генератора нелинейных циклических функций неограниченного аргумента. Так, при расчете переходных режимов в механизмах, приходится рассматривать решение уравнений движения в течение многих циклов для разгона системы до установившейся скорости.

Сущность методики заключается в том, что вместо переменной ф вводится новая переменная, представляющая ее периодическую функцию, .которая и используется в качестве аргумента нелинейной функциональной зависимости. При таком представлении нелинейной зависимости нет необходимости набора ее на блоке нелинейности для многих циклов, а достаточно набрать ее для одного цикла. При изменении аргумента ф нелинейная функциональная зависимость может быть отработана для неограниченного количества циклов.

В этом случае для каждого цикла производится решение уравнения движения с новыми начальными условиями и повторением нелинейной циклической функции, причем задание начальных условий для последующих циклов обеспечивается автоматически, так как последние соответствуют условиям в конце предыдущего цикла.

Необходимо отметить, что при решении задач для установившегося режима нет необходимости точного определения начальных условий. При задании любых начальных условий для цикла модель автоматически выходит на установившийся режим спустя несколько циклов работы. В качестве периодических функций ;ф могут быть использованы sin ф, cos ф, пилообразная зависимость и др. Выбор используемой периодической функции определяется удобством воспроизведения функциональной зависимости на модели. Поясним сказанное на некоторых практических примерах моделирования циклических нелинейных функций [17].

Рассмотрим применение данной модели для моделирования однозначных нелинейных циклических функций, например, приведенного

момента инерции кривошипно-шатунного механизма. На рис. 3-1,а изображена нелинейная циклическая зависимость приведенного момента инерции /(ф) кривошипно-шатунного механизма от угла поворота вала. Характер изменений кривой /(ф) за период от О до п и от я до 2п принимается одинаковым. На рис. 3- ,б и е изображены периодические функции приведенного угла поворота; iJ; - пилообразная функция, 8тф и со8ф. На рис. 3-2 изображены нелинейные зависимости приведенного момента инерции кривошипно-шатунного механизма /(ф), аргументами которых являются периодические функции угла поворота (соответственно пилообразная функция, sin ф и созф). Для образования пилообразной функции угла поворота ф может быть использована схема, изображенная на рис. 3-3,а.

На вход интегрирующего усилителя подается напряжение, пропорциональное угловой скорости. Выходное напряжение интегрирующего усилителя сравнивается с эталонным напряжением 100 В. При достижении выходным напряжением усилителя значения 100 В срабатывает поляризованое реле РП. Замыкание контакта (РП) ;приводит к разряду конденсатора С, благодаря чему схема приводится в первоначальное положение, соответствующее нулевому напряжению на выходе. Данная схема проста в исполнении, но обладает рядом недостатков. При работе на большой частоте повторения процесса разряд конденсатора должен осуществляться быстро, в противном случае конденсатор не будет успевать разряжаться за время срабатывания реле. Такой разряд конденсатора вызывает нарушение нормальной работы контактов реле. С другой стороны, увеличение постоянной времени реле вводит дополнительную погрешность из-за изменения напряжения на выходе интегрирующего усилителя, соответствующего изменению частоты вращения.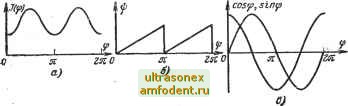

Рис. 3-1. Нелинейная зависимость /(ф) и периодические функции ф.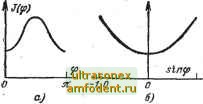

*1,0 -1,0

+ 1,0

Рис. 3-2. Нелинейные зависимости момента инерции кривошипно-шатунного механизма / в функции ф, 81пф в созф.

в случае изменения направления вращения схема значительно усложняется. Функциональная зависимопь, изображенная на рис. 3-2,а, набирается на блоке нелинейности, па вход которого подается пилообразное напряжение с выхода интегрирующего усилителя.

Периодические функции sin ф и cos (р (рис. 3-2,6 и в) могут быть получены с помощью схемы электронного маятника переменной частоты (рис. 3-3,6), зависящей от напряжения.

Схема, приведенная на рис. 3-3,6, может быть использована и в случае изменения знака частоты вращения со. Кроме того, использование периодической функции sin ф или cos ф в качестве аргумента нелинейной

cosinp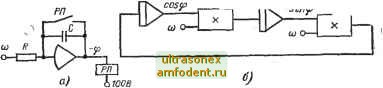

Рис. 3-3. Схемы для моделирования пилообразной функции, sin ф и cos ф.

зависимости /(ф) дает возможность произвести соответствующую деформацию функции (можно растянуть кривую гна участке крутого изменения функции и сжать на участке более пологого ее изменения). Такая деформация кривой часто необходима при наборе ее ,на блоке нелинейности, так как последний позволяет набрать нелинейную зависимость лишь при определенной максимальной крутизне.

При переходе от аргумента ф к периодическому аргументу может быть такой случай, когда функция при одном и том же значении аргумента имеет два различных значения. Принципиально моделирование двузначных нелинейных функций ничем не отличается от моделирования однозначных функций, но требует увеличения количества блоков нелинейности и применения специальной логической схемы для переключений. Релейная схема в определенные моменты времени производит отключение соответствующего блока нелинейности или переключение с одного блока нелинейности на другой. Управление релейной схемой осуществляется с помощью напряжения, пропорционального sin ф или cos ф и отрабатываемого схемой электронного маятника .