Известно, что

(-1)*

(3-5)

при начальных условиях /р(0)-О, если р>0; /р(0) = =1/Г(-Ы)=1, если р=0, и / (0)=0, если р<0, но является целым числом, так как J-nit)=(~l)Jn{t).

Начальные условия для Jp по времени определяются при дифференцировании уравнения (3-5) по времени:

(-l)fe {p + 2k)

К() - 2Р 5j й!r(j)+k+l)

I z 2

Если р>1, то /р(0)=0; если р=0, то Ji(0)=l; если р=п<0, то / п(0)=0.

Уравнение (3-4), преобразованное к виду, удобному для моделирования, имеет вид:

h (-)+/р ()=(1 - ih () - (-)+Pj, ( )

3-5-3. Схема моделирования полинома Лагерра.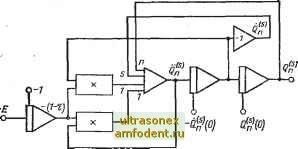

Полином Лагерра Q (t) является решением дифференциального уравнения

с;(о+(+1-ос+< ==о (3-6)

при начальных условиях Q**(0) = 2- -l-3-.....(2n-1); q1>(0) = 0.

При моделировании уравнение (3-6) приводится к виду

=(I -) - (1 - SQ: - СГ-

3-5-4. Схема моделирования полинома Лежандра. ,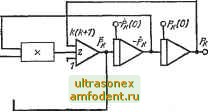

Полином Лежандра Pk{t) описывается уравнением (1 - f) (О - 2tP {t) + k{k-\-\)P{t) = Q.

Это уравнение имеет два линейно-независимых решения: одно, ограниченное на интервале [-1, -fl], определяет полиномы Лежандра, другое решение содержит логарифм и на интервале [-1, -ь1] не ограничено.

Для получения полиномов Лежандра необходимы следующие начальные условия:

при k-2n

При k = 2n-{-1

Р.п. (0)-0; Р, . (0) = 2 (п +1) (-ir\tZ.%X?y Моделируется следующее уравнение:

h it)=-Pk ()+(,) ( 1) (,)

3-5-5. Схема моделирования полинома Эрмита.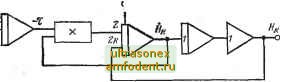

Полином Эрмита образуется решением дифференциального уравнения

Начальные условия определяются следующим образом:

при четном k {k=2n)

Я, (0) = 0; Я, (0) = (--1Г2 -1-3-...-(2п-1); при нечетном k{k=2n-\-l) Н ЛО) = 0; Я, Л0) = 2/г(-1Г-2 .1.3.5.....(2/г-1).

Глава четвертая

СХЕМЫ ЛОГИЧЕСКИХ ОПЕРАЦИЙ, ЗАПОМИНАЮЩИЕ УСТРОЙСТВА, СХЕМЫ КВАНТОВАНИЯ И ПРЕОБРАЗОВАТЕЛИ

4-1. схемы с1>авнения (компараторы)

4-1-1. Схема сравнения.

Компаратор - операционный усилитель, в цепи обратной связи которого имеется лишь элемент ограничения по амплитуде (схема а). Усилитель нельзя использовать без обратной связи (без ограничителя) из-за того, что он выходит из насыщения с запаздыванием.

У усилителя может быть один или несколько входов.

При наличии одного входа усилитель реагирует на