щими коэффициентами и знаками. Здесь (на рис. В-1) и в дальнейшем на приведенных в книге схемах входные и выходные напряжения операционных блоков обозначаются либо в виде входящих в уравнения переменных Xi, tji и т. Д., либо непосредственно в виде напряжений щ. Первые два напряжения образуются на выходах интегрирующих усилителей, а третье воспроизведено с помощью блоков нелинейности и перемножения. Чтобы ввести в схему суммирования напряжения с нужными знаками, используются усилители перемены знака.

При составлении схемы учитывается, что линейные операционные элементы обращают знак выходной величины.

В случае моделирования системы линейных уравнений структурная схема моделирования носит название матричной схемы, так как в модели представлена матрица коэффициентов линейных уравнений. Построение матричной схемы для системы уравнений первого порядка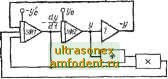

Рис. В-1. Структурная схема моделирования динамической системы, удовлетворяющей уравнению (В-1).

(В-2)

показано на рис. В-2. Для задания коэффициентов разных знаков соответствующая переменная может подаваться на суммирование положительной или отрицательной. С этой целью каждому интегрирующему усилителю придается усилитель перемены знака.

Схема на рис. В-2 состоит из частей, которые не связаны между собой изображениями проводов. Графическое соединение точек схемы заменяется здесь одинаковыми буквенными обозначениями соединяемых электрически точек. Так поступают при построении сложных структурных схем [4]. Полезно, однако, если разделение общей модели на части при ее изображении делается не произвольно, а служит определенным целям. Если изобразить схему рнс. В-1 по принципу схемы рис. В-2,

то получим схему рис. В-3, которую, обобщая, можно привести к схеме рис. В-4. Здесь блоки Фг составляются из операционных элементов по виду уравнений, реализующих функции нескольких переменных на входах интегрирующих усилителей. Математическое описание схемы приведено здесь к системе нелинейных дифференциальных уравнений первого порядка.

Целесообразно стремиться к физически более наглядным способам описания модели и ее схемным изображениям. С точки зрения проверки и настройки модели по частям модель автоколебательной нелинейной системы, удовлетворяющей уравнению (В-1), лучше представить так, как показано на рис. В-5.

В процессе моделирования на этой схеме можно проверить точность набора задачи и компенсировать по-

о- S/nO-

у10-

Ф ,---

УлО-----1

ГГ- Уп

Рдс. В-2. Матричная схема для моделирования системы линейных уравнений (В-2).

Рис. В-4. Обобщенная схема после приведения описания системы к уравнениям первого порядка.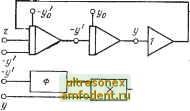

о at

Рис. В-3. Схема для моделиро- Рис. В-5. Модель нелинейной си-вания уравнений первого по- стемы (В-1), предназначенная для рядка (В-1), настройки по частям.

грешности модели. Для этого следует, разделив модель на части по рис. В-5, отьслючить элементы, моделирующие члены затухания (содержащие первую производную). Оставшаяся часть моделирует линейную консервативную колебательную систему с одной степенью свободы. Очевидно, что в этой части модели должны устанавливаться незатухающие гармонические колебания, и если этого не происходит, то только вследствие наличия погрешностей блоков модели, создающих паразитное положительное или отрицательное демпфирование. Эту погрешность можно компенсировать введением величины противоположного знака.

Разделение структурной модели на части, соответствующие отдельным физическим объектам, агрегатам, характерно, в частности, и для моделей систем автоматического регулирования.

При моделировании систем автоматического регулирования часто составляют модели по звеньям, каждое из которых имеет передаточную функцию соответствующего звена натуры, т. е. так, как строится и моделируемая система. Пусть, например, требуется построить модель системы регулирования-(рис. В-6,с), состоящей из следующих направленных звеньев:

объекта регулирования ОР (инерционное звено):

{T,P+)9\{-)\ (В-3)

регулятора Р (колебательное звено):

исполнительного устройства иу (интегрирующее звено):

Т/?е = -7,. (В-5)

Структурная схема модели на рис. В-6,б совпадает со структурной схемой моделируемой системы (Я - модель инерционного звена, К - модель колебательного звена). Схема модели инерционного звена приведена на рис. В-6,е. Модели звеньев высших порядков, в том числе колебательного звена, могут быть получены двумя способами: на одном операционном усилителе по схеме, подобной изображенной на рис. В-6,г, или на нескольких операционных элементах - по структурной схеме уравнения звена (рис. В-6,б). Инвертор на рис. В-6,б нужен при К по рис. В-6,(3.