няется от -1 до +1. Масштаб всех переменных взят равным 100.

t = l, 2,..., п\ Т - Тиакс - 2.

Так как каждый усилитель меняет знак, воспроизво димая схемой функция преобразуется к виду

и поэтому начальные условия на всех интегрирующих усилителях равны -1 (-100 В).

3-4-2. Схемы, воспроизводящие функции ьшах=

Для схемы a: xe для схемы б: х = \ х =А; а.= \1е ,

макс

где е* соответствует Чакс! делитель а на схеме б не показан.

Значения лгаг можно получить лишь на ограниченном интервале времени 0<Т<Тмакс.

При этом решаются определяющие уравнения:

схема а: = ~kx ; схема б: -=kx, при начальных условиях Xi{0)=l.

3-4-3. Схема, воспроизводящая функцию л=1п.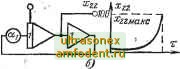

мaкc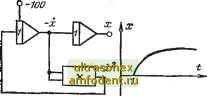

Схема решает определяющее уравнение

[dz)

где t - новая переменная, определяемая из выражения =лг+1. Начальные условия:

.(0) = 0, т. е (0)=1; х{0) = 0; ~Ф) = 1.

3-4-4. Схема, воспроизводящая функцию x=ig t.

Схема решает определяющее уравнение

2х

при начальных условиях х(0)=0 (0)=1. Схема работает в ограниченном диапазоне изменения f(0<<Jt/2). ai= =cos?(l макс ); макс<л;/2.

3-4-5. Схема, воспроизводящая функцию A;=:ctg.

Схема решает опре-}}ао <fioo деляющее уравнение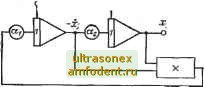

dt

Схема работает в ограниченном диапазоне изменения t: Gxt2~ti, причем i>0, tz<n, t=x+ti, где

т - машинное время. При <ti=n-iz начальные условия имеют вид:

, = 2clgf,; . = 11Г7Г-

Начальные условия х и dxjdx есть одновременно и максимальные значения этих переменных.

3-5. схемы генераторов некоторых специальных функций времени

3-5-1. Схема, дающая возможность возводить в п-ю степень выражение т-Ы и извлекать корень п-й степени из этого выражения.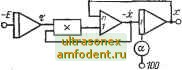

Решение уравнения

(х-\-1)х - пх=0... (3-3)

при начальном условии х(0) = 1 имеет вид ; = (t--l) . Например, решая уравнение (т--1)л; - 5х=0, получаем

х={х-\-1у, а решая уравнение (i--l);--jg-A;=0 при

13 / - -

тех же начальных условиях, получаем x=i/ (t--l) . При моделировании уравнение (3-3) приводится к виду

х= - хх-{-пх. На схеме а=-~.

макс

3-5-2. Схема моделирования специальной функции Бесселя.

Jp(t)

функция /р(0 является решением дифференциального уравнения

(3-4)