части появляются большие коэффициенты, которые трудно задать на АВМ:

Поэтому Fi{-) формируется на входе операционного? усилителя с разомкнутой цепью обратной связи, который служит для отслеживания старшей производной (схема а). Для исключения самовозбуждения возмож* но включение в цепь обратной связи конденсатора не большой емкости.

Второй способ. Для формирования правой части используется предварительное преобразование уравнение (схема б).

В уравнении прибавляют и отнимают л;( >, а затеье разрешают уравнение относительно д; );

д(п)=(1 а )х( )+Л(л;( -), X, х).

Используя суммирующий усилитель с дополнитель- ной положительной обратной связью с коэффициентоле в~1, решают уравнение в неявном виде. Схема требует мер по обеспечению устойчивости.

Третий способ. Уравнение разрешается относительноа инерционного звена (схема в):

= f - X + / (.)1.

Т. е.

(Гр+1)х( - = Р2(д;( -2), ...,х, x)=-Fii ).

Емкость конденсатора С в цепи обратной связи уси* лителя выбирается в соответствии с значением а /е ь и масштабом времени.

5-1-4. Схема четырехквадрантного устройства деления, обеспечивающая воспроизведение функции z-xjyi

путем минимизации функции F - ~-{yz - xf.

При постоянном значении у напряжение z следит за входным сигналом х с некоторым запаздыванием-.. Постоянная времени цепи запаздывания, обратно пропорциональная коэффициенту усиления k-ljn&i, в пе

ле обратной связи обычно весьма мала. Исходное значение г(0) =л;(0)/(0) должно быть точно задано.

UZ-X

р0--z(01=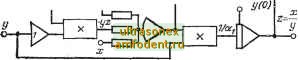

Оперируя с делителем у любой полярности, схема воспроизводит соотношение

ky(yz - x).

Схема допускает одновременное прохождение через нуль делимого х и делителя у. При минимизации F= = \yz-х\ второе множительное устройство заменяется аналоговым переключателем. Уравнение, решаемое схемой, принимает вид:

dz di

= - kys\(yz - x).

5-2. интегрирование по невременному аргументу

5-2-1. Схема интегрирования по невременному аргументу- по машинной переменной л;(т).

e = Jyrf.+2(0) = J()dx + z(0).

Интегрирование по машинной переменной х(х) возможно в тех случаях, когда в модели имеется напряжение, пропорциональное производной по времени х{х).

Погрешность определяется в основном точностью блоков перемножения.

5-2-2. Схема моделирования функции =з1пл;.

Схема основана на решении определяющего дифференциального уравнения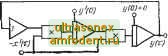

с начальными условиями

(0)=0; (0) = 1. 5-2-3. Схема моделирования функции

Основана на решении вспомогательного уравнения dy!dx-\-by=0, преобразованного к виду

В схеме

а,=Ь; 02=1(0)1. 5-2-4. Схема воспроизведения функциональной зависимости

у=\пх(х).

}1D0siqnllnx(O)]

I0osign[lnxfo)]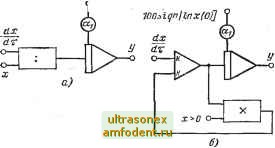

Схема основана на решении вспомогательного определяющего уравнения

dy d-z di X

Ограничения: л;>Л и незнакопеременный; ai= =\пх{0).