раллельных ему шроводников, расположенных в той же ллоско-сти ПО обе стороны от центрального проводника. Электромагнитная волна распространяется вдоль .щелей между проводящими поверхностями. Распределение полей В линии показано на рис. 10.6,6.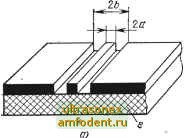

Рис. 10.6. (КОпланарвая линия: а-попереч.ное сечение; б - раопределение полей

Перечисленные выше достоинства щелевой линии справедливы и для копланарной линии.

Волновое сопротивление копланарной линии, вычисленное с помощью Квазистатического приближения, равно

ZbVI = 133,2K{R)/K{R), (10.14)

где R=[l+{b-а)/а]~; 2а - ширина центрального проводника; 2Ь - расстояние между двумя заземленными пластинами.

Волновое сопротивление копланарной линии практически не зависит от толщины подложки. На рис. il0.7 представлена зависимость волнового сопротивления от отношения а/Ь при различ-

Hbfx 8 в .предположении бес-Zb, конечно толстой подложки.

I Г~1 I I I I I Влияние экранирующего 300 -v корпуса, IB который, как пра-

dsCi--к-J-1-1-1-1-1 вило, помещается микросхема, оказывается незначительным, если -его внутренняя поверхность располагается относительно поверхности проводников на расстоянии, большем, чем удвоенная Ширина щели.

Связанные линии. Связанными линиями называют две или .несколько линий передачи, между которыми имеется непрерывная распределенная по длине электромагнитная связь. Они

0,Г 0,1 0,3 0,fy 0,5 0,6 0,7 a/b

Рис. 10.7. Графики аавдаимости волнового сопротивления .копланарной линии от а/Ь и е

широко применяются в различных схемах фильтров, резонаторов, направленных ответвителей, фазовращателей и т. д.

Рассмотрим широко используемую в СВЧ микросхемах пару связанных (ПОЛОСКОВЫХ линий передачи (рис. 10.8,0) при возбуждении их с двух входов одинаковыми по амплитуде волнами напряжений: синфазно (четно) и противофазно (нечетно). На рис. 10.8,6, в изображена конфигурация ©лектрического поля в поперечном сечении, получаемая соответственно при четном и нечетном видах возбуждения.

Рис. 10.8. Структура электрического поля , связанных симметричных полооковых линий: а - пара связанных полосковых линий; б четное возбуждение в - нечетное возбуждение

При четном виде возбуждения токи в обоих проводниках равны и одинаково направлены, а три нечетном виде возбуждения - равны и противоположно направлены. Важным результатом исследования связанных линий лри таком возбуждении является то, что очень сложный анализ пары взаимодействующих между собой линий может быть эквивалентно заменен достаточно .простым рассмотрением изолированных линий, работающих при четном и нечетном видах возбуждения. При этом вводятся параметры Zee и Zbo - волновые сопротивления каждой линии соответственно при четном и нечетном видах .возбуждения.

Сопротивления Zee и Zbo ПОЗВОЛЯЮТ связать электрические характеристики линий с их конструктивными размерами. Эти сопротивления, так же как и волновое сопротивление Zb одиночной линии, могут быть выражены через емкости Све и Сво на единицу длины линии:

(10.15>

- для линии с четным видом возбуждения;

2 = 1/-ифоС,о (10.16)

- для линии с нечетным видом возбуждения;

2в=1/фСв (10.17>

- для одиночной линии.

Для сравнения величин емкостей и соответствующих им волновых сопротивлений обратимся к рис. 10.8. При четном виде

I 247

возбуждения (рис. 10.8,6) емкость Све каждого проводника относительно заземленных оснований меньше, а при нечетном (рис. 10.-8,в) Сво -больше, Чем емкость Св проводника одиночной линии такого же размера. Следовательно, Волновые сопротивления находятся в следуюш,ем соотношении: 2ве>2в>2во-

С целью анализа или синтеза связанных линий необходимо найти связь волновых сопротивлений 1ве и Zbo с геометрическими размерами линии. Эта связь для симметричной полосковой линии определена номограммами Кона [46] (см. рис. 10.9, 10.10).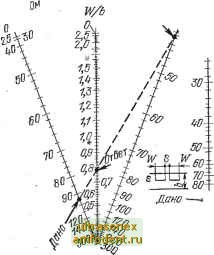

500,-

W S W

70--

60-г 50%

-тЮО -:80

],\100

ZQOr Отдет 300-

0,75 l-OJ 0М д,05

° to~~-30

100Z

tool

-дане

Рис. 10.9. Номограмма завиоимости волно-вых сопрогивлений связанных си-мметричных иолоаковых линий при четном и нечетном видах воэбуж,дения от Wlb

Рис. 10.10. Номограмма зависимости врлновых сопротивлений связанных оимметрнчиых полосковых линий при четном и .нечетном видах возбуждения от S/b

При анализе этих линий, когда известными являются геометрия линий ;(5, W, Ь) и диэлектрическая проницаемость среды е, значения 2ве и Zbo однознзчно определяются при совместном использовании двух номограмм. Если же .проводится синтез по известным характеристикам волновых сопротивлений, то каждая из но-мограмм дает однозначные определения W/b (рис. 10.9) и Sfb (рис. 10.10).

Связанные микрополосковые линии нашли широкое примёне-ние в интегральных схемах фильтров, направленных ответвите-лей, резонаторов. Электромагнитное поле, окружающее и связывающее линии, частично находится в воздухе, а частично в диэлектрике подложки (см. рис. 10.11). При четном виде возбуждения распределение электромагнитного поля показано на рис. 10.11,6, а при нечетном виде возбуждения - на рис. Ю.П.е, Расчет такой пары линий проводится на основе различных числен-