Ньютона (биномиальные переходы) или пропорционально полиномам Чебышева (чебышевские переходы). В первом случае переход имеет максимально плоскую характеристику (рис. 6.20), во втором случае характеристика имеет колебательный характер в полосе пропускания перехода (рис. 6.21). Сравнительный анализ характеристик показывает, что чебышевский переход имеет большую крутизну фронтов частотной характеристики затухания при такой же длине, однако уступает биномиальному переходу в линейности фазочастотной характеристики.

Как для чебышевских, так и для биномиальных переходов результаты расчетов представлены в виде таблиц [8], с помощью которых определяются нормированные сопротивления ступенек, а следовательно, и геометрические размеры перехода.

6.9. ПЛАВНЫЕ ПЕРЕХОДЫ

В плавном переходе, в отличие от ступенчатого, волновое сопротивление линии меняется не скачками, а непрерывно вдоль всей линии, т. е. плавный переход, по существу, является нерегулярной линией, в которой волновое сопротивление является функцией продольной координаты. Плавные переходы могут рассматриваться как предельный случай ступенчатого перехода, у которого число ступенек стремится к бесконечности, а длина каждой ступеньки - к нулю.

От чебышевского и биномиального переходов можно перейти к соответствующим плавным переходам, при етом чебышевский плавный переход будет иметь наименьшую длину из всех типов плавных переходов при одинаковых требованиях к коэффициенту отражения.

Одной из часто используемых разновидностей плавных переходов является экспоненциальный переход, у которого волновое сопротивление изменяется вдоль оси по экспоненциальному закону.

Малых величин коэффициента отражения можно достигнуть в экспоненциальных переходах лишь при длине 1= (2--3)Кв, однако вследствие простоты изготовления, а также большей пробивной прочности, чем у ступенчатых переходов, они находят достаточно широкое применение.

6.10. ПЕРЕХОДЫ С ОДНОГО ТИПА ВОЛНОВОДА НА ДРУГОЙ

На практике часто встречаются случаи, когда необходимо соединять линии передачи или устройства, сконструированные на базе отрезков линии, имеющие разные формы сечений и разную структуру электромагнитного поля. Устройства, осуществляюшие сопряжение волноводов различных видов с преобразованием волны одного типа в другой, также называются переходами.

Переходы этого типа создаются по принципу возбуждения одной линии другой с помощью возбуждающих устройств (щелей, отверстий, штырей и др.) или по принципу постепенного измене-

ния структуры поля и создания условий для быстрого затухания трансформируемого типа волны. Хорошее согласование переходов достигается в ограниченном диапазоне частот и при отклонении частоты от расчетной ухудшается за счет нарушения правильной трансформации волн и появления реактивной составляющей входной проводимости перехода. Характеризуются переходы типом, размерами и волновым сопротивлением соединяемых линий передачи, типом волн в линиях, минимальным Кст в рабочей полосе частот, допустимым изменением фазы сигнала, -минимальными потерями рабочего типа волны, допустимой мощностью и др.

Одним из наиболее распространенных переходов является ко-аксиально-волноводный переход, примеры конструкций которого показаны на рис. 6.22. Они применяются для подключения к вол-новодным устройствам коаксиальных кабелей или других коаксиальных устройств, во вращающихся соединениях и т. д.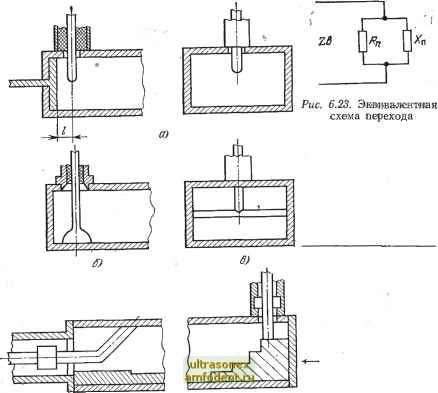

Рис. 6.22. Примеры конструкций коаиоиально-ф волноводных переходов

Действие этих переходов основано на возбуждении отрезка волновода электрическим или магнитным излучателем, служащим элементом связи между коаксиальным и прямоугольным волноводами. При этом Т-волна в коаксиальном волноводе трансформи-

руется в волну типа Ню в прямоугольном волноводе. Для обеспечения минимального значения /Сет перехода в его конструкции предусматриваются согласующие элементы.

Эквивалентная схема перехода показана на рис. 6.23. Для согласования перехода необходимо уравнять активную составляющую сопротивления перехода Rn (см. рис. 6.23) и волновое сопротивление линии Zb, а также компенсировать реактивную составляющую сопротивления перехода Хп. В конструкциях переходов согласование осуществляется с помощью выбора .места расположения и геометрических размеров возбуждающего устройства и с помощью согласующих элементов в виде короткозамкнутых настраиваемых или ненастраиваемых отрезков линий (рис. 6.22,й, б, в), ступенчатых переходов (рис. 6.22,г, д) и др.

Следует отметить, что все выше рассмотренные переходы являются взаимными устройствами. На рис. 6.24 в качестве примера пр.иведен сборочный чертеж коаксиально-волноводного перехода.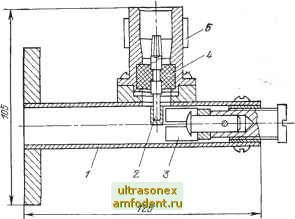

Рис. 6.24. Обо.рочный чертеж коа1наиально-во.лно-.воднош перехода:

1- волновод; 2 - штырь связи; 3 - короткозамыкающий поршень; 4 - диэлектрическая втулка; 5-коаксиальный разъем

Более широкую полосу рабочих частот имеют переходы, у которых проводник излучателя соединен с емкостным штырем (рис. 6.22,в), а также переходы, у которых снижение волнового сопротивления прямоугольного волновода до уровня сопротивления коаксиальной линии достигается с помощью вкладыша, преобразующего прямоугольный волновод в низкоомный П- или Н-волновод (рис. 6.22, г, д).

Недостатком переходов с коаксиального волновода на прямоугольный волновод с электрическими излучателями штыревого типа (рис. 6.22,а) является заметное снижение пробивной прочности волновода за счет концентрации электрического поля на конце штыря.

Более высокие уровни мощности выдерживают переходы с излучателями магнитного типа, особенно с колоколообразным креп-, лением проводника (рис. 6.22,6).