pa только местами векторов Е и Н. Выражение для составляющих поля элементарного магнитного вибратора в дальней зоне совпадает с (9.5) и (9.6) с заменой Е а Я Я на - / на /м и &а на [Ла:

£=-i-sinee- (9.10)

e=i5Гsinee-i (9.11)

где /м - амплитуда магнитного тока, представляющая собой произведение тангенциальной составляющей напряженности электрического поля у поверхности вибратора Е. на его периметр поперечного сечения. Структура поля элементарного магнитного вибратора совпадает со структурой поля вибратора Герца с той лишь разницей, что линии вектора Е, образуя концентрические окружности с осью вибратора, лежат в азимутальной плоскости, а линии вектора Н лежат в меридиональной плоскости. Форма диаграммы направленности и характеристики направленности элементарного электрического и магнитного вибраторов одинаковы. Мощность излучения, полученная так же, как и в предыдущем случае, определяется выражением

Поскольку магнитный ток имеет размерность напряжения, то излучаемую мощность удобно определять через проводимость =0,502 Ям. Сравнивая последнее с (9.12), получаем

Свойства элементарного магнитного вибратора реализуются в элементарной электрической рамке (петле) и элементарной излучающей щели.

Элементарная электрическая рамка (рис. 9.4,6) создает электромагнитное поле, линии магнитной составляющей которого проходят перпендикулярно через плоскость петли, а линии электрического поля лежат в плоскости петли или параллельно этой плоскости. Магнитный ток рамки /м равен подводимому к ней напряжению. Структура поля рамки с размерами во много раз меньше Хо и ее направленные свойства одинаковы со структурой поля и направленными свойствами элементарного электрического и магнитного вибраторов. Излучаемая мощность и сопротивление излучения рамки определяются уравнениями (9.1.2) и (9.13) с заменой I на действующую высоту рамки ha=2nS/7, где 5 - площадь рамки.

Элементарный щелевой вибратор (рис. 9.5,а) можно представить как бесконечно тонкую металлическую пластинку безграничных размеров, в которой прорезана щель длиной t и шириной Д, где Д</<Хо.

Электромагнитное поле элементарного щелевого вибратора по своей структуре совпадает с полем элементарного магнитного вибратора с тем отличием, что линии электрического поля в но-луиространстве / направлены навстречу линиям Е в полупространстве (рис. 9.5,6). Это различие несущественно, так как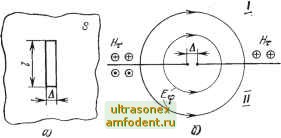

® ® S

Рис. 9.5. Элементарный щелевой излучатель: а - общий вид; б - структура поля

оба полупространства независимы. Магнитный ток в щели равен удвоенному напря1жению между краями щели /м=2[/щ. Мощность излучения щели определяется уравнением (©.12). Если выразить эту же мощность через проводимость излучения, то получим Рх0,5 и\. Сравнивая (9.12) и последнее уравнение, находим

3 Zc \ Ло /

и для свободного пространства, где 2с=120я,

(9.15)

Элементарный излучатель Гюйгенса может быть представлен как элемент фронта плоской волны, магнитное поле которого Я ==Яое** можно заменить эквивалентным электрическим током I=HqAx, а электрическое поле £п=£ое* - эквивалентным магнитным током / =-ЕоАу. Пусть элемент плоской волны имеет прямоугольную форму, площадью As=AyAx. Расположим эле-

Рис. 9.6. Элементарный

излучатель Гюйгенса: а - расположение относительно координатной онстемы; б-диа11ра1М(ма иаправленноспн

Ей I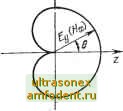

мент и векторы Е и Н относительно координатных осей так, как показано на рис. 9.6,а. Поле, создаваемое таким элементом, равно сумме полей, создаваемых расположенными перпендикулярно друг другу элементарным электрическим вибратором с током / и элементарным магнитным вибратором с током /м. Комплексные амплитуды напряженностей электрических полей, создаваемых отдельно каждым из вибраторов, можно вычислить с помощью формул (9.5) и (9.10) соответственно. Суммируя эти поля [41], можно определить абсолютную величину вектора Е, которая в этом случае будет равна

\Ео\ As

(l-fcosB).

(9.16)

Из этой формулы следует, что элемент Гюйгенса обладает направленными свойствами. Его ДН (рис. 9.6,6) имеет максимум, направленный вдоль оси z, перпендикулярной площадке As. Из (9.16) следует, что ДН элементарного излучателя Гюйгенса является кардиоидой и определяется соотношением

O,(0) = (l-f cose)/2. (9.17)

9.5. ВИБРАТОРНЫЕ АНТЕННЫ

Вибраторные антенны относятся к числу наиболее простых типов антенн. В СВЧ диапазоне они используются как возбудители антенных устройств или как элементы сложных устройств с дискретными излучателями (антенных решеток). Вибраторы, как антенны., чаще всего используются в длинно-, средне- и коротковолновой частях радиодиапазона {43].

К наиболее распространенным конструкциям вибраторных антенн относятся электрические (рис. 9.7,а, б) и магнитные (рис. 9.7,6, г) четверть- и полуволновые вибраторы. Физика их работы и основные свойства полностью соответствуют ранее описанным элементарным вибраторам. Полу- и четвертьволновый электрические вибраторы можно рассматривать как разомкнутую линию

л 20... ifO

Рис. 9.7. Консгрунщия вибраФоров: а - несимметричный электрический; б - симметричный электрический; в - несимметричный MaimHTHbifi; г -1С1имметрич.ный магнитный