Используя понятие коэффициента отражения, можно записать величину напряжения в любой точке линии в следующем виде:

f/ = + f/oxp = /лал + /пал Г е(Ф +2Р). (4.29)

Это выражение может быть представлено векторной диаграммой рис. 4.4.

Из основного уравнения передачи (4.4) напряжения падающей и отраженной волн на сопротивлении нагрузки линии длиной t могут быть представлены уравнениями:

U, = \U{l)+Z,I{l)y2r U={U{l)-ZJ{l)y2. Следовательно, коэффициент отражения нагрузки линии

и ы и

Зная, что и (/) =I(t)Zs, найдем

Гк н - (н

-2b)/(Zh + Z,).

(4.30) (4.31)

(4.32)

(4.33)

чая:

Рассматривая (4.33), можно выделить три характерных слу-

1) Z =Zb, Гкн=0, т. е. в линии без потерь, нагруженной на сопротивление, равное волновому отраженные 1волны отсутствуют;

2) Z =0, Гкн=-1, т. е. при коротком замыкании линии отраженная волна напряжения по амплитуде равна падающей и находится в противофазе с ней, а коэффициент отражения равен минус единице;

3) Z = oo, Гкн=1, т. е. при разомкнутой линии отраженная волна напряжения синфазна и

-- также по амплитуде равна падающей, а- коэффициент отраже-Рис. 4.4. Векториая диаг.рамм-а на- дя равен единице пряжений в длинной линии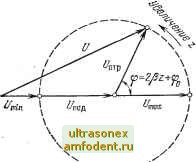

4.6. ВХОДНОЕ СОПРОТИВЛЕНИЕ ЛИНИИ БЕЗ ПОТЕРЬ

Для определения входного сопротивления линии без потерь (Zbx) длиной /

воспользуемся соотношениями (4.11) и (4.12):

г/о u{i) cos (р г)-f 12/(0 sin (р I)

/(Ocos(PO-fi(f 0/-ZBsin(P /)

7

Полагая Z = U{l)II(l), получаем

Uo , l-fi(ZB/ZH)tg(P I)

i + i(Z /ZB) tg(PO

Z .=

= Zb

(4.34>

. (4.35)

Найдем зависимости входного сопротивления линии отхарактера нагрузки

на- ее конце.

а) Короткозамкнутая линия {Zb==0, U(l)=0):

ZBi = iZBtg(M)-

(4.36)

Входное сорротивление наротиозамкнутой линии является чисто мнимой величиной при любой частоте. С физ1ической точки зрения это обусловлено отсутствием потерь в линии.

Зависимость входного сопротивления короткозамкнутой лииии от ее длины показана на рис. 4.5. Из 1гр.афика. рис. 4.5 видно, что с помощью иороткозам-нну-той линии можно воспроизвести любое реактивное .сопротивление. Короткозамкнутая линия функциоиирует как иоследовательный резонансный контур при /=(Яв/2)п и как параллельный резонансный контур при /=(Я.в/4) (2п-I);

1б) разомкнутая линия (Zb=oo, L(l)=Q)

(4.37)

Зависимость входного сопротивления разомкнутой; линии от ее длины показана а рис. 4.6i С помощью разоминутой линии, так же как и с помощью задану-той линии, (МОЖНО ,воспро0зв тя любое реактивное сопротивление. Разомкнутая линия функционирует как параллельный резонансный нонтур при/= (Яв/2)пикак пюследовательный резонансный контур при Z= (Яв/4) (2п-1); =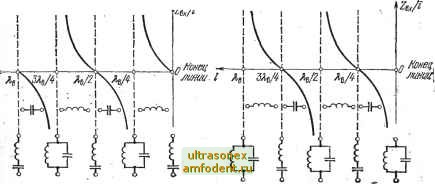

Рис. 4.5. 3.ави№мость .входного сопротивления жороткозамкнутой линии без потерь от ее длины

Рис. 4.6. Зависимость входного сопротивления разомкнутой линии без потерь ют ее длины

в) линия без потерь, нагруженная на реактивное сопротивление. Входное сопротивление линии, .нагруженной а индуктивное сопротивление, в зависимости от ее длины меняется так, как показано на ,рис. 4.7. Из рис. 4.7 вадно, что индуктнвиость L, нагружающая линию, может быть заменена жороткозамшутым отрезком, удлиняющим линию на величину U, которую можно опредешть из уравнения

Btg(P o) = 6>L. . (4.38)

Для случая €Мкостной нагрузки линии без потерь ее входное сопротивление меняется так, как показано на рис. 4:8. Из орэвнекия рис. 4.8 и ряс. 4.6 видао,

что линия без чпотерь при емкостной нагрузке эквивалентна разомкнутой линии, удлиненной на величину /о. Велимина /о может быть определена из уравнения

tg(P/o) = -?BtoC. (4.39)

Таким образом, по входному сопротивлению линию без потерь, нагруженную на чисто реактивную агрузку, можно рассма1тривать как жороткозамкну-тую или разомкнутую линию без потерь, удлиненную на соответствующую ве-личи.ну /о;

Рис. 4.7. Завсишмость входного сопротивления, лииии без потерь, иагруженной а .индуктивное сопротивление, от ее длины

Рис. 4.8. Зависимость входного сопротивления линии без потерь, иагруженной яа емкостное сопротивление, от ее длииы

г) входное сопротивление линии, нагруженной на активное сопротивление. Воопользовавшись (4.35), можно определить входное сопротивление линии, нагружённой на активное сопротивление RkI

1-f i(ZB/j?H)tg(PO

l + i(/?H/ZB)tg(PO

Анализ этого уравнения при различных значениях Ря позволяет сделать следующие выэоды. i

1. Сопротивление нагрузки равно волновому сопротивлению {Rb=Zb). Входное сопротивление (регулярной однородной линии, .нагружеииой яз активное сопротивление, равное ,волноеолту, равно сопротивлению нагрузки: Zsk=Rii=Zb.

2. Сопротивление нагрузки Дольше волнового сопротивления {Rh>Zb). В этом слунае из. (4.33) -следует, что Гн-положительный и фн=0. Следовательно, ма нагрузке падающая и. отра.жениая волны иакодятся в фазе, я у нагрузки будет максимум стоячей волны. В точках максимума, отстоящих от нагрузки на (Лв/2)п, .входное сопротпвленле равно сопротивлению нагрузки: вх=Лтах=?н- В точках минимума, отстоящих от нагрузки на (W4) (2n-1), входное сопротивление

- ; = ?min = ZjR. (4.40)

График завноимости активной и реактивной составляющих полного вход- ного -оопротивлення линии от ее длины при Rh>Z,s показан на рис. 4.9.

3. Сопротивление нагрузки меньисе волнового сопротивления (?н<2в). При условии, что Rk<:Zb, согласно (4.33) Гн - отрицательный и фн=я. Следовательно, на нагрузке падающая и отражённая волны находятся в противофазе и у...нагрузки будет минимум стоячей волны. .В точках минимума, отстоящих от нагрузки а /=(Яв/2)п, входное сопротивление линии paiHHO .оопротивленлю на-