в соответствии с этой диаграммой ека = е (1 -itg6) =

cos 6

(2.G)

tg6 = (T/(o)eJ.

(2.7)

Отметим, что комйлексная диэлектрическая проницаемость, определяемая выражением (2.5), не учитывает поляризационных потерь в диэлектрике, возникающих в результате периодически изменяющейся поляризации вещества. В справочной литературе эти потери учитываются в приведенных экспериментальных значениях tg6, которому соответствует некоторое эффективное значение проводимости о, отличное от проводимости диэлектриков на постоянном токе.

В зависимости от характера параметров е, Ца и а среды можно классифицировать следующим образом.

Среды, обладающие одинаковыми свойствами во всех точках, называются однородными. Среды, параметры которых задаются функциями координат, называются неоднородными. Среды, свойства которых не зависят от величины поля, называются линейными. Среды, параметры которых являются функциями напряженностей электрического и магнитного полей, называются нелинейными. Среды, свойства которых не зависят от направления векторов напряженности поля Е и Н, Назьгвакутся изотропными. Среды, параметры которых меняются в зависимости от изменения направления векторов магнитного и электрического поля, называются анизотропными.

Ниже, за исключением специально оговоренных случаев, рассматриваются явления в однородных, линейных и изотропных средах.

тричеокая проницаемюсть

2.3. УРАВНЕНИЯ МАКСВЕЛЛА И ИХ ФИЗИЧЕСКИЙ СМЫСЛ

В технике СВЧ чаще всего Используются рассматриваемые ниже уравнения Максвелла для гармонических колебаний [2, 3].

Так же, как и в технике низких частот, в диапазоне СВЧ при анализе гармонических процессов применяется метод комплексных амплитуд, при котором векторы поля и другие величины, изменяющиеся во времени по гармоническому закону, например поле

заменяются комплексной амплитудой*

Е = Е е* = £,е М, + £ ,е .1, + £

где Етх, Ету, Emz - амплитуды отдельных составляющих поля, являющиеся функциями пространственных координат х, у, z; фж, фу, 4>z - их фазы.

В общем случае в электродинамике используется четыре уравнения Максвелла, но в случае гармонических электромагнитных полей система этих уравнений для комплексных амплитуд сводится к двум первым уравнениям. Два других уравнения, представляющие собой обобщение законов Гаусса для электрического и магнитного полей, в случае гармонических колебаний вытекают из двух предыдущих.

Первое уравнение Максвелла является обобщением закона полного тока Ампера), согласно которому циркуляция вектора напряженности магнитного поля Н по замкнутому контуру i равна току /, пронизывающему данный контур,

(2.8)

До трактовку! Максвеллом под током / понимался только ток проводимости. Максвелл предположил, что изменяющееся во времени электрическое поле, например поле между обкладками конденсатора (рис. 2.2), также способно подобно току проводимости

>СМ =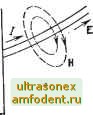

Рис. 2.2. Ток и элек-тромашитное иоле в новденюаторе

создавать магнитное поле. Для качественной оценки этого эффекта Максвелл ввел понятие тока смещения и установил, что плотность тока смещения равна

i, = dD/dt=EodE/dt + dP/dt = edE/dt. (2.9)

Ток смещения состоит из двух составляющих; первая (eodE/dt) соответствует только изменению электрического поля (ток смещения в вакууме); вторая (dP/dt) обусловлена движением связанных в атомах зарядов в результате их поляризации переменным током (поляризационный ток).

Таким образом, рассматривая среду, в которой может распространяться электромагнитная энергия. Максвелл пришел к выводу, что полный ток, создаваемый переменным электрическим по-

* Посколику в книге .рашматриваются только гармоавчеоиие колебания, то овдельныё обозяачеНИЯ для иоашлаксных амплитуд и величин не вводятся.

лем, в этрй среде должен включать в себя как ток проводимости /цр, так и tOK смещения /см: /=/пр+/см.

Первое ухавнение Максвелла имеет следующий вид:

mtH = J p + JeM = (TE + icoe E = itoe E. (2.10)

Первое уравнение Максвелла утверждает: если в некоторой точке пространства существует переменное электрическое поле, соз-даюи{ее токи проводимости и смещения, то в окрестности этой точки возникает переменное вихревое магнитное поле, создаваемое этими токами.

Электрическое поле и создаваемое им магнитное поле образуют правовинтовую систему (см. рис. 2.3).

Рис. 2.3. К первому уравнению Мановелла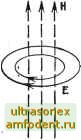

Рис. 2.4. iK iBTqpoMy уравнению Маковетла

Второе уравнение Максвелла является обобщением закона индукции Фарадея.

Фарадей установил, что если через поверхность S, ограниченную проводящим контуром I, проходит меняющийся во времени магнитный поток, то в замкнутом контуре / возникает электродвижущая сила индукции Э, которая равна

Э = -дФт. (2.11)

До Максвелла считалось, что это уравнение справедливо только для случая проводящего контура. Максвелл предположил, что соотношение (2.11) справедливо также и в том случае, если среда не обладает проводимостью.

Физический смысл этой гипотезы сводится к предположению, что всякое изменение магнитного поля во времени непрерывно вызывает (независимо от параметров среды) появление электрического поля.

Для гармонических колебаний второе уравнение Максвелла Записывается в следующем виде:

rotE = -аВ/а = -iwH-H. (2.12)

Второе уравнение Максвелла утверждает: если в некоторой точке пространства существует переменное магнитное поле, то в окрестности этой точки возникает переменное вихревое электрическое