комплексный вектор Пойнтинга, определяющий количество

энергии, протекающей в единицу времени через единичную площадку, перпендикулярную направлению потока энергии. Направление П определяется направлением движения буравчика, рукоятка которого вращается от Е к Н. Вектор Пойнтинга характеризует интенсивность излучения электромагнитной энергии; средняя за период плотность мощности излучения

n,p = 0,5Re[E, Й]. (2.27)

2.7. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ И ПРОВОДНИКАХ

Рассмотрим электромагнитное поле плоской однородной волны, распространяющейся в неограниченной однородной изотропной среде.

Тип волны (плоская, сферическая, цилиндрическая и др.) определяется формой волнового фронта. Волновым фронтом называется поверхность равных фаз электромагнитной волны. Если поверхности равных фаз и равных амплитуд совпадают, то такие волны называются однородными. В соответствии со сказанным, плоской однородной электромагнитной волной называется волна, у которой поверхности равных фаз и амплитуд являются одной и той же плоскостью.

Выберем Декартову систему координат с направлением оси г, совпадающим с направлением распространения волны. Особенностями свойств плоской однородной волны является отсутствие продольных составляющих электромагнитного поля (£z=-f/z=0), векторы поперечных составляющих являются взаимно-перпендикулярными прямыми линиями (Е=£ж; И=Ну), вектор Пойнтинга перпендикулярен волновому фронту.

Волновое уравнение (2.18) для составляющей Ех в рассматриваемом случае

dEjdz + kE = Q. (2.28)

Решение этого уравнения для неограниченной среды, в которой возбуждена бегущая волна (волна, распространяющаяся в направлении оси z), будет следующим:

Ех(г)Е,е-У-. (2.29)

Аналогично для магнитной составляющей

Ну{2} = Нг,уе-Уг-. (2.30)

Запишем решение волновых уравнений (2.29) и (2.30) в тригонометрической форме:

. .(2, /) = £ ,е- со8(со-рг-Ьф1); (2.31)

Hy{z, 0 = Я г,е- со8(со-рг-ф2). . (2.32)

На рис. 2.5 приведены графики, соответствующие последним уравнения.м. Эти графики представляют собой картину распределения электромагнитного поля плоской однородной волны при f=const для случая, когда в среде отсутствуют потери (а=0). Из рисунка видно, что векторы электрического и магнитного полей взаимно-перпендикулярны, а их величины в пространстве вдоль оси Z меняются по гармоническому закону.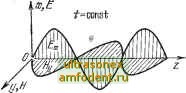

Рис. 2.5. Рашред-еление составляющих поля вдоль бои Z в плоской од-лородиой электромагнитной волне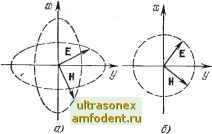

Рис. 2.6. Поляризация поля плооиих однородных волн: а - эллиптическая; б -Жруговая

Поляризация электромагнитного поля. В принятом нами расположении координатных осей (рис. 2.5) вектор Е всегда колеблется в плоскости XOZ. При этом конец вектора Е в плоскости, перпендикулярной направлению распространения и неподвижной относительно его самого, описывает прямую линию. Волна, обладающая этими свойствами, называется линейно-поляризованной. Плоскость XOZ называется плоскостью поляризации.

Предположим, что волна возбуждается двумя когерентными источниками со взаимно-перпендикулярными направлениями одинаковых по величине векторов Е. В этом случае конец суммарного вектора Ej; в зависимости от фазового угла ф между составляющими векторами будет описывать прямую при ф=0, эллипс при фтО (рис. 2.6,а) или окружность ф=90° (рис. 2.6,6). Аналогично и наименование волн: с линейной поляризацией, с эллиптической и круговой. В зависимости от направления вращения вектора Е д различают волны с правой (вектор вращается по часовой

стрелке) и левой (вектор Е вращается против часовой стрелки) поляризацией. В обоих случаях для определения направления вращения необ.ходимо смотреть навстречу волне.

Заметим, что любую волну с вращающейся плоскостью поляризации можно представить как суперпозицию двух сдвинутых по фазе и в пространстве линейно-поляризованных волн.

Когда плоская волна не является однородной, т. е. когда по-вер.хность равных фаз не совпадает с поверхностью равных амплитуд, поляризация может быть различной в разных точках плоскости, перпендикулярной направлению распространения волны.

Основные характеристики электромагнитного поля.

1. Коэффициент распространения - величина, характеризующая изменение амплитуды и фазы бегущей электромагнитной волны. Под бегущей волной будем понимать электромагнитную волну определенного типа, распространяющуюся в линии передачи только в одном направлении. Коэффициент распространения находится путем подстановки решения однородного волнового уравнения (2.29) в волновое (2.28):

y\E + kE, = 0 или {y\ + kE,Q.

Эти уравнения удовлетворяются при условии

y\k = Q, т. е. vi=i = i(0l/8 ,tx,. (2.33)

Из (2.33) следует, что коэффициент распространения yi является комплексной величиной и для плоских однородных волн на заданной частоте определяется только параметрами среды.

2. Коэффициент затухания определяет уменьшение амплитуды электромагнитной волны при прохождении одного метра пути и при размерности в децибелах на метр (дБ/м) равен действительной части коэффициента распространения, умноженной на 8,68:

ttg = 8,68 (иУы V-a sin (6/2) = 8,68 аУг ц /со8 б sin (6/2). (2.34)

3. Коэффициент фазы определяет измерение -фазы волны при прохождении одного метра пути. Коэффициент фазы в радианах на метр (рад/м) равен мнимой части коэффициента распространения:

р = аУы tacos(6/2) = соl/e7lVcos6cos(6/2). (2.35)

4. Фазовая скорость - скорость перемещения фронта гармонической волны. Гармоническая волна описывается уравнением

Ех {г, t) = Е, е- cos (со /-р г-f ф). (2.36)

Волновой фронт этой волны, как плоскость постоянных фаз, не меняющихся при движении, должен удовлетворять уравнению (at-p2 = const. Для бесконечно малых изменений и г аиИ-dz= = 0 ли iudt=dz. Пользуясь обычным определением скорости, найдем, что фазовая скорость плоской волны

v = dzldt = (sil. (2.37)

С учетом (2.35) можно записать

Фо= 1/[Клйссо8 (6/2)]. (2.38)

5. Длина волны - расстояние, пройденное волной за период колебания Я=ифоГ. Используя соотношения Г=2я/со, (2.37) и (2.38), получаем

Я = 2я/р; (2.39)

к = 2я/[со1/ёлсо8б cos (6/2)]. . (2.40)