2 Коэффициент фазы, равный мнимой части коэффициента распространения, определяется формулой

P = co/LC. (4.13)

3 Коэффициент затухания, равный действительной части коэффициента распространения, определяется формулой

а= {R/2) УШ+ (G/2) У1{С = -f сс. (4.14)

ад =(/?/2)l/C/L (4.15)

коэффициент затухания, обусловленный тепловыми потерями в

проводниках;

e = (G/2)yZ7C (4.16);

- коэффициент затухания, обусловленный потерями в диэлектрике (изоляции).

4. Длина волны Определяется с помощью (2.39):

= 2я/р = (2я/(о) YLC. (4.17)

5. Фазовая скорость волны определяется с помощью (3.23):

u$ = co/p=l/T/LC. (4.18)

6. Волновое сопротивление обычно определяется с помощью (4.7).

4.4. СТОЯЧИЕ ВОЛНЫ

Под стоячей волной принято понимать периодическое изменение амплитуды напряженности электрического поля (напряжения) и амплитуды напряженности магнитного поля (тока), вызванные интерференцией падающей и отраженной волн в линии передачи. В рассматриваемом случае это можно представить следующим образом. Допустим, что в регулярной линии без потерь распространяются падающая [/под и отраженная f/отр волны напряжения одинаковой амплитуды, т. е.

f/na (z, 0 = п>со5((о/-рг), (4.19)

/отр(г, O = fmcos((of-f pz). (4.20)

в результате интерференции этих волн образуется стоячая волна напряжения, описываемая уравнением

(2. 0 = С/шд(2, ) + f/oxp(2. 0 = 2t/ cos(co0cos(pz), (4.21)

и, аналогично, стоячая волна тока, описываемая уравнением

I (г. t) = / зд (г, О - /отр (г, О = 2 sin (ш t) sin (р z). (4.22)

Рассмотренные стоячие волны в реальных условиях возника-К)т при нагрузке линии на реактивное сопротивление, коротком замыкании или полном размыкании линии. Во всех этих случаях

.волна напряжения отражается с противоположным знаком по отношению к волне тока, этим объясняется знак минус в (4.22). На рис. 4.2 показано распределение напряжения вдоль оси z в стоячей волне. Анализируя график рис. 4.2 и уравнение (4.21), можно -сделать следующие выводы о свойствах стоячей волны напряжения:

1) амплитуда напряжения 2f/mCOs(p2) стоячей волны вдоль jiHHHH меняется по гармоническому закону;

2) в точках, где р2= (2п-1)я/2, амплитуда напряжения равна нулю; эти точки называются узлами;

3) в точках, где р2=пя, амплитуда напряжения максимальна к.равна 2Ит\ эти точки принято называть пучностями;

4) расстояние между соседними пучностями и соседними узлами равно половине длины волны передаваемых колебаний.

Аналогичн&е выводы можно сделать и относительно стоячей волны тока.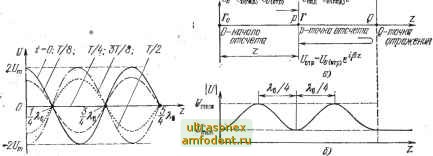

Рис. 4.2. Распределение стоячей Рис. 4.S. Частично стоячая волна в ли-волны (напряжения в линии нии:

а-распре деление характерных точек; б - райпределение напряжения

4.5. ЧАСТИЧНО СТОЯЧИЕ ВОЛНЫ И КОЭФФИЦИЕНТ ОТРАЖЕНИЯ

Под частично стоячей волной следует понимать суммарную волну, образующуюся в результате интерференции отраженной и падающей волн неравных амплитуд.

Рассмотрим длинную линию без потерь и отражений на конце. Допустим, что в некоторой точке Q имеется нерегулярность (рис. 4.3,а), отражающая часть энергии .падающей волны. В этом случае в сторону источника сигнала направится отраженная волна по амплитуде меньше падающей. При этом условии слева от точки Q (см. рис. 4.3,6) установится частично стоячая волна. Частично стоячие волны принято оценивать с помощью коэффициента отражения по напряжению (напряженности электрического по-

, -г или С помощью коэффициента стоячей волны /Сет*. Первый пставляет собой отношение комплексных амплитуд напряже- я /напряженности электрического поля) отраженной и падающей волн в заданной точке линии передачи:

Г = Геф = { шд, (4.23)

а второй -отношение напряжений (напряженности электрического поля) в максимуме и минимуме частично стоячей волны (см. рис. 4.3,6), т. е.

тах пад1 IotpI Ь Г 1л \

1г/пад1-отр 1-Г

Такое определение Гк и /Сет правильно, если точка отражения определена однозначно. В диапазоне СВЧ понятие точка отражения неоднозначно, так как обычно мы имеем область искажения поля, вызванную наличием неоднородностей. Однако вдали от места искажения появившиеся отраженные волны и вся физическая картина явлений подобны тому, когда эти отражения происходят в определенной плоскости (точке) сечения линии, что позволяет использовать приведенное определение коэффициента отражения на СВЧ.

Выразим коэффициент отражения в любой точке линии через коэффициент отражения в начале линии, представив последний соотношением

где С/о(пад) и f/o(oTp) - напряжсния отраженной и падающей волн в начале линии.

Запишем напряжения падающей и отраженной волн в произвольной точке Р (рис. 4.3,й) через соответствующие напряжения падающей и отраженной волн в начале линии:

f/пaд = f/o(пaд)e-P (4.25)

f/oTP = f/o(oTp)eP. . (4.26)

Используя эти соотношения, перепишем уравнение (4.23) для коэффициента отражения в любой точке линии в следующем виде:

г ГрФ -/ III - 0 (отр) р i2B2 .

о(шд)е-Р

Учитывая, что коэффициент отражения в начале линии

Гно = Id 6 получим Г еф = Гое* (ФоН-25г) (4

означает, что

Г = Го и Ф = Фо + 2рг. (4.28)

* В книге яопользуется коэффициент стоячей волны только яо алряж-ению, SMecToV Р заяиси двпущено сокращение в его обозначении (Кст