9.4. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Любую излучающую антенну можно рассматривать как состоящую из множества элементарных излучателей. Это позволяет воспользоваться таринципом суперпозиции и определить поле антенны как сумму полей элементарных излучателей. Поля самих элементарных излучателей находятся по заданному распределению тока с помощью решения уравнений Максвелла. Обычно полагают, что величина тока не меняется вдоль длины элементарного вибратора. К влементарным излучателям относятся: влемен-тарный электрический вибратор (диполь Герца), элементарная электрическая рамка (магнитный диполь), элементарная щель и излучатель Гюйгенса.

Элементарный электрический вибратор - диполь Герца - показанный на рис. 9.i2,a, представляет собой тонкий проводник с шарами на концах. Шары создают емкость, которая позволяет получить постоянную амплитуду тока вдоль проводника.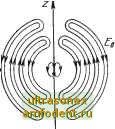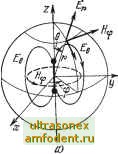

/ту,

Рис. 9.2. Поле диполя Герца: а -в ближней зоне; б - электрическое в дальней зоне; в - магаитное в дальней зоне

Решение уравнений Максвелла для электромагнитного поля диполя Герца позволяет получить следующие уравнения [2]:

4л 111

sin бе-

kr \kr j \kr j

=-ikr

sin e e

-ikr

(9.2) (9.3) (9.4).

где / - амплитуда возбуждающего тока вибратора; 1 - длина вибратора; к=ш КваРа - волновое число или коэффициент распространения плоской волны; г - расстояние от излучателя до TQ4iKH наблюдения.

Из (9.2) - (9.4) следует, что вектор напряженности электрического поля диполя Герща имеет две составляющие Ег я Ев , ко-

торые лежат в плоскости, проходящей через его ось, а вектор напряженности магнитного поля- одну Яф, которая лежит в плоскости, перпендикулярной его оси. Характеристики антенн определяются, как правило, для дальней зоны, которой соответствует расстояние г Хо/2я. При этом условии в уравнениях (9.i2) - (9.4) можно пренебречь {IjkrY и {IjkrY, переписав их в следующем виде:

Zc sin I

a-ikr

Sin e e-

(9.5) (9.6)

Таким образом, в любой точке пространства вектор электрического поля вибратора Герца имеет одну составляющую Ев, лежащую в меридиональной плоскости (плоскости, проходящей через ось вибратора); в любой точке пространства вектор магнитного поля имеет также одну составляющую Яф, лежащую в азимутальной плоскости (плоскости, перпендикулярной оси вибратора); в силу независимости составляющих поля от угла ф структура поля остается одинаковой в любой плоскости, проходящей через ось вибратора. Структура поля вибратора Герца в дальней зоне (рис. 9.2,6, в,) соответствует структуре поля сферической волны, где поверхности равных фаз образуют концентрические сферы с центром в начале координат (в середине вибратора); Ев и Яф взаимно-перпендикулярны; отнощение Ев равно характеристическому сопротивлению- волны Zc.

Из (9.5) следует, что приведенная ДН вибратора Герца в меридиональной плоскости

Oi(e) = £e/ax = sine (9.7)

представляет собой две касательные окружности, центры которых лежат на прямой, перпендикулярной оси вибратора и проходящей через его середину (рис. 9.3,а). В азимутальной плоскости величина напряженности электрического поля не зависит от угла ф, следовательно, Ф1(ф) =£<р/£max=il, и ДН представляет собой окружность с центром на середине вибратора (рис. 9.3,6).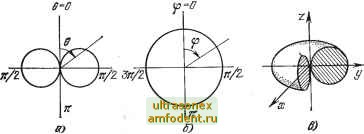

Рис. 9.3. Диаграмма направленности диполя Герда: плоскости .вибратор ; б--в плоскости, перпендикулярной в,и€рагору; в-Простран!СТВенна.я -форма

Пространственное изображение ДН элементарного электрического вибратора показано на рис. 9.3,в.

Средняя за период плотность потока энергии согласно (2.27) равна

Пср = -Re[EH] = -(- ) ZpSine,

где * обозначает комплексно-сопряженную величину.

Из этого уравнения следует, что излучение электромагнитной энергии максимально в направлениях, перпендикулярных оси вибратора (е=я/2), и не .зависит от угла ф. Вдоль своей оси (6=.0 или ie=il80°) вибратор не излучает.

Мощность, излучаемая элементарным электрическим вибратором,

/>.=jn <i.s=i(ii-yzjfsin.ede<i..

Выполнив вычисления и принимая 2с=120я, получим

Р = А0пЦ111\)\ (9.8)

.Эта же мощность, выраженная через сопротивление излучения, Pj, =:0,5/2/?2- Сравнивая это выражение с предыдущим, можно определить сопротивление излучения:

/?2 = 80лМг№ (9.9)

Элементарный магнитный вибратор. Физическую модель элементарного магнитного вибратора (рис. 9.4,а) можно получить, если взять стержень из материала с магнитной проницаемостью значительно больше магнитной проницаемости окружающей среды, например из феррита. В качестве возбуждающего устройства можно использовать петлю, обтекаемую током проводимости. Постоянство вектора магнитной индукции Б вдоль стержня обеспечивается с помощью шаров на концах.

На основании инвариантности уравнений Максвелла можно утверждать [41], что элементарный магнитный вибратор отличается по структуре поля от элементарного электрического вибрато-

/ / /

I : \

-tp I I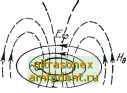

/ \

Рис. 9.4. Элвм.ента,рный мага-итный вибратор: а - физическая МОяель; бэлементарная рамка