Глава 17. Анализ и моделирование мультисервисной нагрузк Л 7.4, Проектирование нагрузки для участка ЦСИО

17.4. Проектирование нагрузки для участка ЦСИО

1. Постановка задачи. .

Когда известно количество каналов V на некотором участке сети задача проектирования нагрузки заключается в определении допуо тимого числа Л/, потоков нагрузки для каждой категории пользовате лей / = 1, п, при условии, что соблюдаются установленные требова ния к качеству обслуживания вызовов (норма вероятности потерь р,).

С математической точки зрения, сформулированная задача являет ся неопределенной, поскольку имеется п неизвестных (Л/, при / = 1, п) l канальные ресурсы могут в разных пропорциях распределяться межд соответствующими потоками нагрузки разных категорий. Для исключЦ ния этой неопределенности потребуем, чтобы искомые величины был пропорциональны некоторым заранее заданным числам, т.е.

= x=const

(17.12I

Такой подход широко распространен при исследовании систем т( летрафика с неоднородными потоками нагрузки, когда с помощью некоторой совокупности коэффициентов пропорциональности задается так называемый профиль нагрузки - к--.кг: ... :кп. В результате требуется определить единственную неизвестную величину х, через которую выражаются все искомые переменные:

Ni=xki,

(17.13)

при / = 1, л.

Ниже предлагается один из способов приближенного решения поставленной задачи проектирования нагрузки для участка ЦСИО. При этом используется метод эквивалентных замен, описанный в разделе 17.4.1, а также процедура условного разделения пропускной способности пучка.

2. Расчет коэффициента скученности объединенной нагрузки.

Применение метода эквивалентных замен предполагает вычисление коэффициента скученности поступающей нагрузки. Для каждой категории источников нагрузки (/ = 1, л) интенсивность Я./суммарного потока вызовов будем определять по формуле Л = Л а где а, - интенсивность индивидуального потока вызовов /-й категории. Подставляя это равенство в (17.9), можем записать:

т - =1

(17.14)

После преобразования правой части (17.14) с учетом (17.13) окончательно получим

(17.15)

Таким образом, коэффициент скученности не зависит от количественного состава потоков нагрузки разных классов, а определяется только профилем нагрузки, с помощью которого задается относительный вес калодой категории.

3. Расчет нормы на средние потери вызовов.

В мультисервисных системах уровень качества обслуживания вызовов нормируется отдельно для каждого вида предоставляемых услуг, поэтому требования к потерям вызовов на участке ЦСИО записываются в виде совокупности неравенств я, р/, где / = 1, п , Следовательно, с учетом формулы (17.11) должны выполняться неравенства

(17.16)

при / = Гл. В неравенствах (17.16) присутствует единственная неизвестная величина я, поэтому рассматриваемую систему неравенств перепишем в следующем виде:

TlZk

(17.17)

Решением системы (17.17) служит неравенство я < min( p;/m,),

и отсюда вытекает, что величину

с

i rrii

(17.18)

можно принять за норму для средних (общих) потерь вызовов.

4. Метод условного разделения пропускной способности пучка.

Для нахождения неизвестной величины х, которая присутствует в выражениях (17.12) и (17.13), применим следующий метод [9], идея которого в графической интерпретации содержится в [10] (§ 17.5).

Случай л = 2. Обозначим через F{NuN2) среднюю вероятность потерь для рассматриваемого пучка как функцию от числа индивидуальных потоков нагрузки. Неизвестные значения Л/i и Л/г должны Удовлетворять уравнениям

N,/k, = N2/k2, (17.19)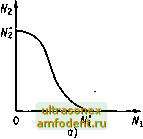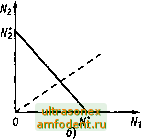

и окончательно

Рис. 17.1. Отношение размеров потоков нагрузки двух категорий при фиксированной вероятности потерь

F{NuN2) = p. (17.20)

Уравнение (17.20) задает некоторую линию на плоскости с координатными осями Л/, и Л/г (предполагается, что в общем случае количество потоков нагрузки может принимать и нецелое значение). Точки пересечения этой линии с осями координат (рис. 17.1, а) определяются из уравнений F(/\/i*,o) = p и f{o,N2 )= р, которые соответствуют случаям, когда пучок обслуживает вызовы только одной категории.

Линию на рис. 17.1, а, которая изображает зависимость FiNNz) = р, приближенно заменим прямой линией, проходящей через точки (л/,*,о) и (о,Л/2 ). Эта прямая, которая задается уравнением

n; л/г

(17.21)

показана на рис. 17.1, б вместе с пунктирной прямой, соответствующей уравнению (17.9). Таким образом, приближенным решением поставленной задачи, которая математически записана в виде уравнений (17.19) и (17.20), будут координаты точки пересечения двух прямых, представленных на рис. 17.1, б.

Для получения результата в аналитическом виде необходимо решить систему линейных уравнений

/с, кг /Vi , Л/г

n; л/г*

= 1.

(17.22)

С помощью подстановки Л/, = х - к,-, /=1,2 находим

З1+З2

Л/,=/С,/(Р,+Р2).

где р, = /с,/л/; ,/=1,2.

Общийслучай (л > 2). Аналогично изложенному выше, при каждом / = 1, л , можно рассмотреть воображаемую ситуацию, когда суммарный поток состоит только из вызовов /-Й категории. В этом случае поступающая нагрузка равна У= Л/,а/т,/7,и имеет коэффициент скученности Zk = т,. Следовательно, по формуле (17.10) можно определить вероятность потери вызова:

% = Е

Наибольшее значение N при котором выполняется равенство

, Л/,а;/),

(17.23)

и, соответственно, соблюдаются заданные требования к качеству обслуживания вызовов, обозначается как Л/* и полностью характеризует пропускную способность рассматриваемого пучка каналов относительно нагрузки Ай категории.

Уравнение (17.23), из которого определяется величина N*, решается путем подбора с помощью таблиц Пальма. Если число V/гп; нецелое, то необходимо произвести интерполяцию.

При совместном обслуживании вызовов нескольких категорий будем предполагать, что средняя вероятность потерь останется в норме, если допустимое количество потоков нагрузки каждой категории взять пропорциональным соответствующей величине NJ, т.е. Nj = р,Л/*, где Р/ есть доля пропускной способности пучка, которая при ее условном распределении отводится нагрузке /-й категории. Очевидно, что должно выполняться условие

п Л/.

5:з.=5:=1-

1=1 /=1 л/,

Отсюда с учетом (17.27) получаем

и окончательно

/=1 N,

(17.24)

5. Алгоритм проектирования нагрузки для участка ЦСИО.

Для определения допустимого числа индивидуальных потоков мультисервисной нагрузки, которые обслуживаются полнодоступным пучком каналов при известной емкости пучка и заданных требованиях 1 к качеству обслуживания вызовов, необходимо выполнить следую-1 щую последовательность действий.

1. По формуле (17.15) вычислить коэффициент скученности поступающей нагрузки (Zk).

2. С помощью формулы (17.18) найти норму на средние потери, вызовов (р).

3. Решая уравнение (17.24) при / = 1, л, определить пропускную спо-, собность пучка каналов относительно нафузки Ай категории (Л/*).

4. Используя формулу (17.24), рассчитать коэффициент х, через! который устанавливается взаимосвязь между профилем мулвтисер-1 висной нагрузки и численностью соответствующей группы потоков.

5. Вычислить с помощью соотношения (17.13) допустимое число] индивидуальных потоков нагрузки /-й категории (/ = 1, л), округлив по-1 лученный результат до целого числа.

6. Численный пример.

Пусть проектируемый участок ЦСИО, на котором предусмотрен пучок емкостью 1 = 30 каналов, обслуживает вызовы двух категорий 1 (л = 2) при профиле нагрузки 2:1, т.е. /с, = 2 и /сг = 2. Требования к качеству обслуживания вызовов формулируются следующим образом: Pi = 0,03 и Рг = 0,08. Необходимо определить допустимое число потоков нагрузки, которые характеризуются параметрами, приведенными в табл. 17.2.

Решение поставленной задачи осуществляется в соответствии с алгоритмом, изложенным выше в данном разделе.

1. Вычисляем коэффициент скученности поступающей нагрузки:

Z - h,+mlkz azhz (l 2-4-180-н4 1-320)/3600 * mkah+nrizkzazhz (1-2-4-180-н4-1-3-20)/3600

2. Находим норму на средние потери вызовов:

р = zmin

= 2,5 min

0,03 0,08 1 4

= 0,05.

3.1. Для определения пропускной способности пучка каналов относительно нагрузки 1-й категории запишем уравнение (17.23):

Таблица 17.2. Параметры потоков нагрузки

Е(30/1, Л/, х4х 180/3 600) = 0,05.

По таблицам Пальма находим, что при 1= 30 и У = 24,8 имеет место E(V,Y) = 0,05. Следовательно, 0,2/Vi = 24,8 и отсюда вытекает, что N; =24,8/0,2 = 124.

3.2. При / = 2 уравнение (17.23) выглядит следующим образом:

Е(30/4, Л/2хЗх120/3 600) = 0,05.

По таблицам Пальма с использованием интерполяции получаем, что при V= 7,5 равенство E(V,Y) = 0,05 выполняется в случае, когда /=4,14. Поэтому 0,1Л/2 = 4,14 и N2 =4,14/0,1 =41,4.

4. Производим расчет по формуле (17.24):

х = 1/

1 2

n; N2

124 41,4)

= 24,82.

5. Применение соотношения (17.12) дает следующий результат: Л/, = x/fi = 24,82x2 = 49,64 и Л/2 = хк2 = 24,82x1 = 24,82. С учетом правил округления окончательно получаем: Л/, = 50 и Л/г = 25.

Контрольные вопросы

1. Перечислите каналы стандартного доступа в ISDN сетях.

2. Приведите определение марковского процесса.

3. Объясните понятие скученности нафузки.

4. Характеристика нафузки.

5. Особенности метода эквивалентных замен для расчета потерь вызовов.

Список литературы

1. ШнепсМ.А. Системы распределения информации. Методы расчета; Справочное пособие, - М.: Связь, 1979.

2. Ершов В.А., Кузнецов Н.А. Метод расчета пропускной способности матостралей мультисервисных телекоммуникационных сетей Труды MAC (приложение к журналу Электросвязь ). - 1999. - № 1(9). - С. 22-24,

3. Ершов В.А., Ершова Э.Б., Ковалев В.В. Метод расчета пропускной способности звена Ш-ЦСИС с технологией ATM при мультисервисной обслуживании Электросвязь. - 2000. - № 3. - С. 20-23.

4. Корнышев Ю.Н., Фань Г.Л. Теория распределения информации; Учебное пособив для ВУЗов. - М.: Радио и связь, 1985.

5- Корнышев Ю.Н., Пшеничников А.П., Харкевич А.Д. Теория телетрафика. - М.: Радио и связь, 1996.

6. Lindberger К. Simple approximations of overflow system quantities for additional demands in the optimization Proc. 10th Int. Teletraffic Congr., Section 5.3, Paper 3. -Montreal, 1983.

7. FrederickB A.A. СолдезИоп in blocking systems; a simple approximation technique BSTJ. - 1980. - Vol. 59, N. 6. - P. 805-827.