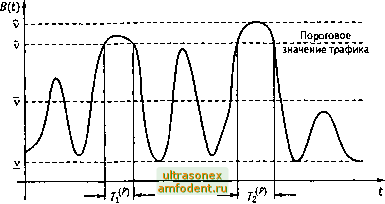Рис. 1.1. Основные параметры мультимедийного трафика

ITU-T [2, 3]. Эти характеристики описывают интегральные параметры случайного процесса B{t), пример реализации которого приведен на рис. 1.1.

К характеристикам трафика, который генерируется различными мультимедийными услугами, относятся следующие:

- значения трафика (мгновенное, максимальное, пиковое, среднее и минимальное), бит/с;

- коэффициент пачечности трафика (пульсация);

- средняя длительность пикового трафика;

- средняя длительность сеанса связи;

- форматы элементов трафика;

- максимальный, средний, минимальный размеры пакета;

- интенсивность трафика запросов.

Максимальное значение трафика v. Максимальное число блоков информации, которое соответствующий сервис генерирует в единицу времени, определяется как:

v = maxe(f).

Пиковое значение трафика. Трафик соответствующего сервиса, который превышает установленный для него пиковый порог v .

Среднее значение трафика v. Среднее число блоков информации, которое соответствующий сервис генерирует в единицу времени, определяется как

V =

B(t)dt,

где г - длительность сеанса связи.

Минимальное значение трафика у. Минимальное число блоков информации, которое соответствующий сервис генерирует в единицу времени, определяется как

v = minS(0.

Коэффициент пачечности трафика К. Определяется как отношение между максимальным и средним трафиком соответствующего сервиса. Коэффициент пачечности вычисляется по формуле:

-<р)

Средняя длительность пика Т . Средняя длительность интервала времени, в течение которого, соответствующий сервис генерирует пиковый трафик, вычисляется по формуле:

где Л/ - число пиков в течение сеанса связи; т; - длительность f-пика процесса B(t), / = 1,Л/<, а длительность /-пика определяется выражением

г-(Р) ±(в) As)

где t t, - моменты начала и окончания /-пика, которые определяются следующими выражениями:

= min t, Z, = min где /i , Z = 0.

B(()>v B(()>v

Перечисленные выше параметры используются для описания трафика соответствующего сервиса в течение одного сеанса связи с абонентом сервиса.

Интенсивность запросов X на получение обслуживания абонентами сети у соответствующего сервиса определяется как среднее число поступивших запросов на обслуживание в единицу времени.

Средняя длительность сеанса связи - средняя продолжительность интервала времени, в течение которого соответствующий сервис обслуживает поступивший запрос.

Максимальный размер пакета s - максимальный размер элемента трафика в битах (элемент трафика передается адресату как единое целое).

Таблица 1.1. Параметры трафика мультимедийных услуг (типичные значения)

Средний размер пакета s - средний размер элемента трафика в битах.

Минимальный размер пакета s - минимальный размер элемента трафика в битах.

Некоторые типичные параметры трафика, генерируемого соответствующими источниками, приведены в табл. 1.1.

1.3. Понятие о самоподобном трафике

Многочисленные исследования, проведенные за последнее десятилетие учеными разных стран, позволяют утверждать, что трафик современных телекоммуникационных сетей с коммутацией пакетов обладает особой структурой, не позволяющей использовать при проектировании привычные методы, основанные на марковских моделях и формулах Эрланга, которые хорошо себя зарекомендовали как аппарат для проектирования телефонных сетей с коммутацией каналов. Игнорирование этих особенностей телетрафика приводит к недооценке нагрузки и к неоправданно оптимистическим решениям.

Особенности, о которых идет речь, вызваны проявлением эффекта самоподобия телетрафика [4]. В самоподобном трафике присутствует некоторое количество достаточно сильных выбросов на фоне относительно низкого среднего уровня, что значительно увеличивает за-

держки и джиггер при прохождении самоподобного трафика через сеть, даже в случаях, когда средняя интенсивность трафика намного ниже потенциально достижимой скорости передачи в данном канале.

Самоподобные процессы относятся к процессам с длинной памятью, что позволяет предсказать их будущее, зная относительно недавнее прошлое. Заметим, что прогнозирование телетрафика чрезвычайно важно при разработке алгоритмов работы сетей, обеспечивающих повышение качества обслуживания (QoS). Для провайдеров услуг прогнозирование загрузки сетей позволяет планировать их своевременное развитие.

К настоящему времени показано, что самоподобной структурой обладает трафик в проводных сетях при использовании широко распространенных протоколов Ethernet, ОКС 7, VoIP, ТОР и др. Аналогичные эффекты обнаружены в сотовых телефонных сетях с коммутацией пакетов. Исследования, результаты которых представлены в [6], подтверждают наличие самоподобных свойств и в трафике современных телекоммуникационных сетей, использующих технологии беспроводного доступа IEEE 802.116.

Приведем далее, следуя [5], некоторые математические выкладки, иллюстрирующие особенности самоподобных процессов.

Пусть X = (Xi, Хг, ) - полубесконечный отрезок стационарного в широком смысле случайного процесса дискретного аргумента (времени) tE N = {1,2...}. Обозначим через ц < . и ст < > среднее и дисперсию процесса X соответственно, а через

- автокорреляционную функцию и автоковариацию процесса X. Так как процесс X - стационарный в широком смысле, среднее ц, дисперсия D[X] = = Ь(0), коэффициент корреляции г{к) и автоковариация Ь{к) не зависят от времени tv\ г{к) = г{-к), Ь(к) = Ь(-к).

Допустим, процесс X имеет автокорреляционную функцию следующего вида:

г(к)~ к-Ц(к), к-ос, где О < 3 < 1 и Li - медленно меняющаяся на бесконечности функция, т. е. lim / = 1 для всех х > О (примерами медленно меняющейся

функции могут служить Li(0 = const, Li(0 = log(O)-

Обозначим X = (Х!; , ...) - усредненный по блокам длины т процесс X, компоненты которого определяются равенством

X< > (1/т)( X . , +...-ь ), т, 6 Л/.

В дальнейшем изложении будем называть такой ряд - агрегированным. Обозначим через г (/с), Ь (/с) и V = Ь (0) коэффициент корреляции, автоковариацию и дисперсию процесса Х * соответственно.

Приведем ниже определение строго самоподобного в широком смысле процесса.

Определение. Процесс X называется строго самоподобным в широком смысле [ССШС] (exactly second-order self-similar) с параметром Н=1 -(3/2), 0<р<1, если

Гг (к) = г{к), keZ, me{2,3,...},

т. е., что ССШС процесс не меняет свой коэффициент корреляции после усреднения по блокам длины т.

Другими словами, X - ССШС, если агрегированный процесс Х неотличим от исходного процесса X, как минимум, в отношении статистических характеристик второго порядка.

Определение. Процесс X называется асимптотически самоподобным в широком смысле (АСШС) [second-order asymptotical self-similarity] с параметром Н = 1 - (р/2), О < р < 1, если

\]т r(k) = g(k), /се Л/.

Смысл этого определения состоит в том, что X является АСШС процессом, если после усреднения по блокам длины т и при m -> > он сходится к ССШС процессу.

Вместе с понятием ССШС существует понятие просто самоподобного процесса, которое для большего терминологического различия мы будем называть самоподобным в узком смысле процессом СУС.

Определение. Процесс X называется самоподобным в узком смысле (СУС) [strictly self-similarity] с параметром Н = 1 - (р/2), О < Р < 1, если справедливо выражение

т- Х = X. me/V,

которое понимается в смысле равенства распределений. Связь между процессами ССШС и СУС аналогична связи между процессами, стационарными в широком и узком смыслах.

Для описания самоподобных процессов иногда используют термин хэрстность . Хэрстность определяется коэффициентом (экспонен-той) Хэрста. Этот коэффициент {Н) определяет степень самоподобия.

1/1сследуя по летописям за 800 лет годы разливов Нила, Хэрст обнаружил, что существовала тенденция, когда за годом хорошего наводнения следовал еще один плодородный год, и, наоборот, за годом малой воды следовал еще один голодный год. Другими словами, казалось, что появление голодных и плодородных лет - неслучайно. Для подтвер>адения данного факта Хэрст ввел коэффициент О < Н < 1,

который в его честь сейчас называется коэффициентом (экспонентой) Хэрста. В случае независимости друг от друга уровней ежегодных разливов, логично было бы представить процесс разливов обычным броуновским движением с независимыми приращениями, которое

3 рассмотрено [5], при этом коэффициент Хэрста Н = 0,5. Однако, как

; обнаружил Хэрст, для Нила Н = 0,7.

Одним из способов вычисления коэффициента Н является анализ так называемой R/S статистики (нормированного размаха). Обозначим -ежегодный уровень воды в Ниле, тогда средний уровень воды за т лет:

/=1

Получим новый (кумулятивный) ряд, представляющий сумму за время f ежегодных колебаний уровня Нила относительно среднего M[t,]:

(1.1)

При этом диапазон между максимальным и минимальным значениями X(f,T) за время тобозначим Я(т):

R(T) = max(X(f,T)-minX(f,T)), 1Ф/Фт. (1.2)

Тогда R/S статистика определятся безразмерным отношением диапазона Я(т) к стандартному отклонению :

R/S =

Я(т)

Я(т)

(1.3)

Хэрст показал, что для многих природных явлений справедлива зависимость:

Я(т)

lS(x)}

(1.4)

где с - положительная константа, не зависящая от х.

В частности, если приращения исследуемого временного ряда (1.1) независимы, т. е. ряд представляет собой броуновское движение с независимыми приращениями, то коэффициент Хэрста Н = 0,5. Значение Н для Нила Н ~ 0,7, что подтверждало присутствие некоторой зависимости между последовательными отсчетами /И -i!

Следует заметить, в случае 0,5 < Н < 1 говорят о персистентном (поддерживающемся) поведении процесса либо о том, что процесс обладает длительной памятью. Другими словами, если в течение некоторого времени в прошлом наблюдались положительные приращения процесса, т. е. происходило увеличение, то и впредь в среднем будет