с дисциплиной FS тождественна системе с г, (г, < N) параллельными и одинаковыми обслуживаюидими приборами. При этом, если в СМО С, имеется свободный прибор, то требование обслуживается так же, как и в системе с дисциплиной IS. Но если все приборы за-няты, то вновь поступившее требование получает отказ и с веро-М* ятностью brj переходит в систему С,.

(цДп),/=1,l), если г однородна;

) / ч . г4 -7:;\ к , атрица функ-

(ц,.к(п), /=1,L, /с=1,/<), если Г неоднородна

ций интенсивностей обслуживания требований в сети обслуживания; ц,(п) - функция интенсивности обслуживания требований в системе С, в зависимости от состояния п сети обслуживания; ц к(п) - функция интенсивности обслуживания требований к-го класса в системе С, в зависимости от состояния п сети обслуживания.

(пДп),/=1,l), если г однородна;

/ / ч . гт . - вектор состояния

(л к(п), /=1,L, к=\К), если Г неоднородна

сети обслуживания, где п, - число требований, пребывающих в системе С, однородной сети, а п - число требований к-го класса, пребывающих в системе С, неоднородной сети.

Существующие методы анализа и расчета сетей обслуживания [29] обеспечивают вычисление точных или приближенных значений их характеристик для стационарного режима.

Для однородных сетей обеспечивается вычисление следующих характеристик:

1. Р{п) - распределение вероятностей состояний сети, где п = {ni,

nCi, п е S{/V, L), S(N, L) = (n} - пространство состояний сети Г - множество векторов, каждый из которых определяет некоторое Чразмещение N требований по L системам сети. Мощность про-

ыстранства S(/V, L) равна

. Состояния в S(N, L) лексиграфи-

чески упорядочены. Отношение порядка состояний сети опреДеля-

J ется следующим образом: п* > п\ п={п.....п[},

= .....п[>}, если 3 с?:п>>п\ и V / <с? п{> = п{.

2. Р(п, = S) - распределение вероятностей состояний системы С, вероятность пребывания в системе s требований, V s=0,N.

3. Р(р, = S) - распределение вероятностей числа занятых приборов системы С, - вероятность одновременного обслуживания s требо- ваний в этой системе, V s=0,f,.

4. Р{5, = S) - распределение вероятностей длины очереди системы С,- вероятность одновременного ожидания обслуживания в 04ej реди системы s требований, V s=0,N.

5. т1, - коэффициент использования системы С,.

6. Я, - интенсивность входящего потока требований в систему С,.

7. п, - математическое ожидание числа требований, пребывающих в системе С,.

8. Q, - математическое ожидание числа занятых приборов в системе С,.

9. 6, - математическое ожидание длины очереди требований системы Ci.

10. X, - математическое ожидание длительности обслуживания тре- бований в системе С,.

11. и, - математическое ожидание времени пребывания требований в системе С,.

12. w, - математическое ожидание времени пребывания требований в очереди системы С,.

13. f, - математическое ожидание времени реакции для обслуженных в системе С, требований (длительность интервала времени между моментом окончания обслуживания требования в системе С, и моментом поступления этого же требования в эту же систему).

14. X / - математическое ожидание времени длительности интервала времени от момента поступления требования в систему С, до момента поступления этого же требования в систему С,. Методы расчета однородных замкнутых СеМО общего вида.

Класс СеМО, расчет которых возможен в рамках точных или приближенных методов, определяется сетями, удовлетворяющими условию локального баланса [17, 18]. Условие локального баланса формулируется следующим образом: интенсивность перехода сети обслуживания в некоторое состояние равна интенсивности выхода сети из этого же состояния. Схематически допустимый класс сетей обслужишь

ГА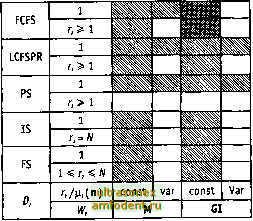

Рис. 16.2. Допустимый класс сетей обслуживания

вания изображен на рис. 16.2: штриховка соответствует наличию то ного метода расчета сети обслуживания, двойная штриховка соотвек ствует наличию приближенного метода расчета сети обслуживани: отсутствие штриховки соответствует отсутствию метода расчета 19-21].

Сети обслуживания, принадлежащие допустимому классу и име1 щие точное решение:

- удовлетворяют условию локального баланса, которое обеспечи ет возможность разложения СеМО на составляющие ее СМО представления стационарного режима сети в виде композиц! стационарных режимов ее систем обслуживания [18];

- являются инвариантными относительно функций распределения длительности обслуживания требований в системах, что обеспечивает возможность использования для вычисления стационарных характеристик СеМО общего вида методов расчета экепоненци-альных сетей [22, 23].

Функционирование СеМО описывается марковским дискретным процессом на конечном множестве состояний

S(/V,i)=

n=(ni....,nL) П1>0, /=1,L, £п,=А/

Распределение Р{п) вероятностей состояний СеМО задается в мультипликативной форме

где п,е п, /;{п/) - величина, пропорциональная вероятности того, что система С, находится в состоянии П/ (в Q пребывает п, требований).

/;.(n,)=- i-, Y((s)=min(s,fi). s=0,W, x,=

Пу/(5)

lii(n) ,

где (0 = {C0i,(Oi) - любое ненулевое решение однородной линейно системы уравнений (О = (Ох Г, а G(W, L) - нормализующая константа, определяемая следующим выражением:

GiN,Lh 2: П,(п,), n,in.

n6S(/V.i)/=1

Расчетные формулы для стационарных характеристик однородн СеМО приведены в табл. 16.1.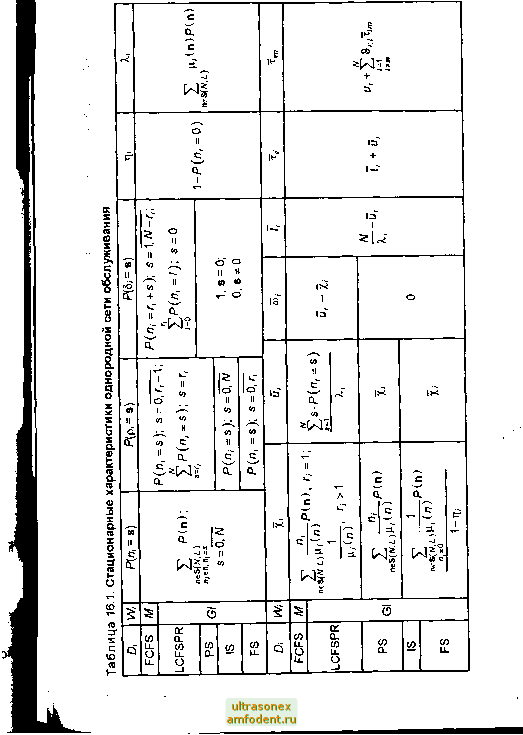

16.2.5. Программные средства математического моделирования

Инструментальная программная среда математического моделирования телекоммуникационных и информационных систем MONAD [9, 10, 20] реализована как процедурное расширение языка программирования общего назначения 6++. Данный подход обеспечивает естественное использование изобразительных средств базового языка программирования для описания сложных алгоритмов функционирования, которые имеют место в вычислительных сетях, планов проведения экспериментов с комплексами моделей, алгоритмов интегрирования результатов модельных экспериментов с моделями комплекса.

Инструментальная среда моделирования MONAD разработана использованием объектно-ориентированной технологии. MONAD пред ставляют собой совокупность открытых для расширения и модифика-; ции библиотек программ, процедур, функций, структур данных, клас- сов, объектно-ориентированных программных интерфейсов, исходных данных, что обеспечивает возможность адаптации алгоритмов MONAD к условиям исследования реальных телекоммуникационных систем, а также развития системы моделирования, как в части их методов, так и в части изобразительных (языковых) средств описания исследуемых систем и используемых алгоритмов моделирования.

MONAD предоставляет средства по организации структуры взаи-, модействующих программных объектов (программ, данных различных типов и классов и их методов), которые образуют программную модель комплекса, описывающую решение сформулированной задачи моделирования.

Построение программной модели осуществляется путем формирования ее множества объектов и установления соответствия каждо-, му модельному объекту концептуальной модели некоторого множест ва объектов программной модели. Так, например, функции или процедуры соответствуют в программной модели образам событий компонентов концептуальной модели, а структуры, классы, переменные моделируют в программной модели состояния, алфавиты и точки траекторий компонентов концептуальной модели.

Любой интервал комплексных или модельных времен концептуальной модели отображается в программной модели интервалом системного времени - интервалом астрономического времени, в течение которого выполняется программный код, моделирующий в программной модели все события, имеющие место на траекториях развития компонентов, определенных на соответствующих интервалах комплексного или модельного времен.

В составе системы математического моделирования MONAD выделяется ряд подсистем, которые разбиваются на три основные класса: 1) базовые; 2) функциональные; 3) объектно-ориентированные.

В классе базовых подсистем определены: 1) система управления программными объектами; 2) система диагностики и обработки запрещенных ситуаций; 3) система управления внешними интерфейсами.

В классе функциональных подсистем определены: 1) система гибридного моделирования; 2)система имитационного моделирования; 3) система аналитического моделирования.

Объектно-ориентированные подсистемы обеспечивают расширение MONAD в сторону описания некоторого класса моделируемых систем (например, мультисервисных сетей).

Базовые подсистемы системы моделирования. Базовые подсистемы MONAD предоставляют функциональным подсистемам сервисные возможности по организации программных объектов в составе программной модели, распределению между объектами программной модели различных системных ресурсов (времени процессоров и оперативной памяти), организации ввода/вывода различного вида данных. К базовым подсистемам относятся: система управления программными объектами, система обработки запрещенных ситуаций и система управления внешними интерфейсами.

Система управления программными объектами. Система управления программными объектами обеспечивает: 1) идентификацию модельных объектов в ПМ; 2) организацию и представление в программной модели множеств произвольных программных объектов, упорядоченных некоторым образом; 3) выполнение произвольных операций над объектами этих множеств в соответствии с их порядком.

Для идентификации объекта в программной модели определяется его идентификатор. Различается основной и системный идентификаторы объекта. Системный идентификатор объекта, в отличие от основного, определяется этой системой автоматически и служит для идентификации данного объекта, когда не определен его основной 1адентификатор. В зависимости от типа объекта в качестве его системного идентификатора могут быть определены: или идентификатор некоторой переменной системы моделирования, или некоторая структура ее данных, или идентификатор ее процедуры или функции.

Основные идентификаторы определяются только для компонентов программной модели, кортежей ее объектов, а также используемых потоков входных и выходных сообщений системы моделирования. Основной идентификатор определяется именем объекта и списком индексов объекта - упорядоченной последовательности (в том числе и нулевой длины) его индексов. Для компонентов одного типа должны быть определены уникальные основные идентификаторы. Для компонентов различных типов могут быть определены одинаковые основные идентификаторы. Два основных идентификатора являются одинаковыми, если совпадают их имена и списки индексов.