в общем случае анизотропной среды или ограниченной изотропной среды смещение частиц в упругой волне имеет компоненты как вдоль, так и поперек направления распространения Соответственно для каждого направления в кристалле имеется три волны со своими скоростями распространения, связанными с компонентами волнового вектора и отвечающими взаимно перпендикулярным смещениям (изонормальиые волны). Фазовые скорости упругих волн в кристаллах сильно зависят от направления распространения, причем анизотропия фазовой скорости отражает симметрию характеристик упругости кристалла. Вдоль направлений и кристаллах, соответствующих плоскостям и осям симметрии и ипо1да совпа-

Таблица 10.3. Температурная зависимость скорости и поглощения ультразвука в натрии, калии и их сплавах [49, 5.5

Молярное сод ер жа-ние

Молярное содержание

Да

377,15 2523 11,7 Na-t-68 % К 293,15 2046 11,1

391,15 2516 12,2

403,15 2513 12,8

420,15 2501 13,2

427,15 2498 13,4

Na+43 % К 293,15 2159 12,3

345,15 2128 9,2

403,15 2095 10,2

338,15 393,15 347,15 381,15 389,15 423,15

2022 2003 1887 1867 1863 1843

10,6 11,7

29,9 33,5 33,3 37,6

дающих с основными кристаллографическими осями, возможно распространение так называемых чистых волн, векторы смещения которых либо коллинеарны волновому вектору, либо нормальны к нем>, В наиболее простом случае кристаллов кубической симметрии скорости 11родолы!ых волн [938]:

[1001 = / -

(Cii+Ci3+2C,4) ,

и поперечных волн:

]/¥

1401 [/ -у-

[1001

(волна поляризована в направлении [001]),

[ПО]

= / 2 (Сц - С12) (волна поляризована в направлении [ПО]),

[111]=)/

где индексы в квадратных скобках обозначают направление распространения волны, Су - модуль упругости,

В поликристаллических материалах скорость (рис, 10.2) определяется модулем упругости и ориентацией зерен. При наличии преимущественной ориентации зерен такие материалы упругоанизотропны.

В ограниченных твердых телах кроме продольной и поперечной волн имеются и другие типы волн: поверхностные, крутильные, изгибные, волны Лэмба, волны Рэлея и другие, скорость которых определяется не только упругими характеристиками вещества, но и геометрией тела. В стержнях, поперечные размеры которых много меньше длины волны и которые получили распространение в ультразвуковой термометрии в ка-i) честве чувствительных элементов и акустических линий связи, фазовая скорость продольных волн v = = V Е/р, т. е. она меньше скорости продольных волн в неограниченной среде [489].

В термометрии используют также крутильные колебания в стержнях и изгибные колебания в пластинах. Фазовые скорости гармонической изгибной волны с круговой частотой 03 = 2я/ в стержне и пластине равны соответственно [948]

4 / ERho, V Р

У 12р (1 - 02)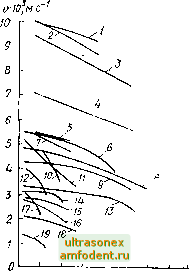

500 /ООО 1500 то 2500 3500 Т К

(R - радиус инерции поперечного сечения стержня относительно оси, Л - толщина пластины).

Эти скорости много меньше фазовой скорости продольных волн. Для изгибных волн характерна дисперсия: при увеличении частоты фазовая скорость возрастает. Групповая скорость згибных волн равна удвоенному значению фазовой скорости [9481.

Крутильные волны в стержнях бездисперсионны, а их скорость распространения [489]

Рис. 10.2. Температурные зависимости скорости распрострапения ультразвуковых колебаний в твердых телах [1425]:

/ - AljOs; 2 - сапфир; 3 - MgO 4 - MgSiO,; 5 -ZrOj -f 8,8 % V2O3 6 - Mo; f - Rh; - Re; 9 - W: 10 - AI; - Ti; /2 - Zn; 13 - Та 14 - Pd; 15 - Pt; 16 - Ag; 17 - Sn 18 - Au; 19 - РЬ

При разработке газовых, жидкостных и твердотельных ультразвуковых термометров нужно учитывать по1лощеиие ультразвуковых колебаний Физическая природа поглощения ультразвука в газах и жидкостях связана с вязкостью и теплопроводностью среды 1948]. Поглощение, об-условлен!юе этими факторами, описывается соотнощением

а = -

ц

Здесь - объемная вязкость, Ц - сдвиговая вязкость, х - коэффициент теплопроводности.

Поглощение, обусловленное сдвиговой вязкостью и теплопроводностью, называется классическим и характеризуется коэффициентом а,,. Часть коэффициента поглощения ар, которая пропорциональна объемной вязкости, связана с релаксационными процессами. Коэффициент объемной вязкости зависит от частоты, поэто.му

1 -f 0)42

где т - время релаксации, - скорость при малых частотах ((от < 1), - скорость при высоких частотах (шт 1). Полный коэффициент поглощения

Величина о,Л (X - длина волны) при частоте релаксации (Ор = 1/т имеет максимум. Релаксационное поглощение всегда сопровождается дисперсией скорости звука, а частотная зависимость скорости имеет вид

й)2т2 1 + (йН

Коэффициент поглощения в газах зависит при данной температуре от отпощепия частоты / к давлению f, так что разрежение газа эквивалентно увеличению частоты. Вклад объемной вязкости и релаксационных процессов, значителен для многоатомных газов, тогда как в одноатомных газах релаксационные процессы отсутствуют и а = а. В газах, как правило, преобладает колебательная релаксация. Даже небольщие примеси посторонних газов заметно влияют на р и Шр. В газах сложного состава имеет место как колебательная, так вращательная релаксация, причем частоты релаксации различаются на несколько порядков.

В жидкостях поглощение ультразвука определяется в основном вязкостью, и здесь существенен вклад релаксационных процессов. Релаксационное поглощение в жидкостях может быть обусловлено колебательной, структурной, поворотно-изомерной релаксацией, диссоциацией. Частота релаксации (Ор, как правило, очень велика и лежит в гиперзвуковом диапазоне [678]. Коэффициент поглощения в жидкостях сильно зависит от температуры. Температурные кривые поглощения имеют максимум, величина и положение которого зависят от частоты. С увеличением последней максимум смещается в сторону высоких температур и величина а растет. В жидких металлах важцый вклад в поглощение вносит теплопроводность. Кроме того, при наложении магнитного поля с индукцией В поглощение возрастает пропорционально величине

vB й)2т2 1

где т =

2ру 1 + 0)42

jx - магнитная проницаемость жидкого металла, v - проводимость. Этот эффект связан с возникновением индуцированных токов в жидком металле под действием ультразвука [948].

В твердых телах наблюдается поглощение и рассеяние ультразвуковых волн, в различной степени проявляющееся для продольных и сдвиговых волн. Поглощение определяется внутренним трением и теплопроводностью среды, причем последняя на поглощение сдвиговых волн в однородных телах не влияет При высоких частотах и низких температурах на поглощение влияет взаимодействие ультразвуковых волн с внутренними возбуждениями в твердом теле: тепловыми колебаниями, электронами, спиновыми волнами и пр. Значение поглощения зависит от кристаллического состояния, наличия дефектов и примесей, от характера технологической обработки материала, от концентрации вакансий и дислокаций. Рассеяние вызывается многократными отражениями и преломлениями ультразвуковой волны на неоднородностях структуры. Затухание ультразвуковой волны в твердом теле можно представить в виде а = а,/ + af*, где первое слагаемое описывает поглощение, второе - рассеяние [190]. При повыще-нии температуры внутреннее трение возрастает и поглощение становится преобладающим фактором затухания ультразвукового сигнала В поликристаллических материалах наблюдаются высокотемпературные релаксационные пики внутреннего трения, связанные с интенсификацией про-0 цессов диффузии и приводящие к уменьшению скорости ультразвука в соответствующем диапазоне температур [1010].

При падении ультразвуковой волны на границу раздела двух сред наблюдается отражение и прохождение волн соответственно с коэффициентами rut, которые определяются из формул Френеля [360, 948]

1 +г

pu/sinO - py/sinS py/sin О* -\- py/sin 9 Spy/sin G

py/sin 0 -\- po/sin e

где p и p--плотности первой и второй сред; у и г/ - скорости в первой и второй средах; G и G- углы между направлениями распространения соответственно падающей и прошедшей волн и плоскостью раздела (считаем, что волна проходит из первой среды во вторую),

10.1. Особенности контактных и бесконтактных термометров. Методы построения резонансных и импульсных термометров

Ультразвуковые термометры в зависимости от вида чувствительного элемента можно условно разделить на контактные, которые содержат специальный чувствительный элемент, вводимый в объект измерения, и бесконтактные, в которых чувствительным элементом служит сам объект измерения (или его часть), через который пропускаются ультразвуковые сигналы; а в зависимости от избранного метода измерения на резонансные, использующие температурную зависимость резонансных свойств чувствительного элемента, и импульсные, в основе которых лежит температурная зависимость временного интервала между ультразвуковыми импульсами. Если метрологические характеристики ультразвуковых контактных термометров определяются физическими свойствами материалов, из которых изготовлены чувствительные элементы, то характеристики бесконтактных термометров определяются параметрами объекта измерения. Существенным преимуществом бесконтактных термометров является то, что здесь иет необходимости в специальном чувствительном элементе, введение

которого может исказить первоначальную картину распределения темпера-тур>1, а возмущения, впосп>гые в объект при про,хождеиии ультразвукового сигнала малой иптспсивпости, настолько несущественны, что их в большинстве случаев не учитывают Если по ряду причин необходима повышенная мощность акустического сигнала, то изменение телшературы за счет его прохождения через объект можно оценить из соотношения [945]

где t - время, Q - добротность, Рд - амплитуда деформации.

Наиболее известным вариантом резопаиспого ультразвукового термометра является кварцевый термометр, чувствительным элементом которого является кристалл кварца. Блок-схема термометра представлена иа рис. 10.3.

Телнтературная зависимость частоты кварца может быть описана соотношением [580]

f{T) = f,(\-\-a.T + T + yT).

Можно найти такой оптимальный срез кристалла, для которого практически исчезают коэффициенты высших порядков и в этом случае частота почти линейью зависит от температуры. Кварцевые термометры строятся в основном на высокочастотных кварцевых резонаторах повернутых Y-срезов, использующих колебания сдвига по толщине. Рабочая частота термочувствительных резонаторов лежит в диапазоне ...30 МГц. Используются как колебания на основной частоте (1...10 МГц), так и колебания на третьем и пятом обертонах (5,..30 МГц). Термочувствительные резо:1аторы обычно помещаются в герметичный корпус, защищающий элемент от осаждения на поверхности резонатора твердых частиц, пыли, влаги, агрессивных веществ. Применение корпуса повышает надежность термодатчика, предотвращает старение пьезорезонатора, снижение его добротности. Практически используются два варианта выполнения термодатчнков: с ваку-умированием резонатора в стеклянном баллоне и с герметизацией резонатора в миниатюрном газонаполненном металлическом баллоне. Герметизированные термодатчики в результате заполнения баллона газом с хорошей теплопроводностью (гелием), применения металлического корпуса и небольших размеров имеют меньшую тепловую инерционность, чем вакуумированные термодатчики, В то же время вакуумированные термо-датчикн характеризуются более высокой временной стабильностью и разрешающей способностью (табл, 10,4), eдocтaткoм кварцевого термометра является наличие гистерезиса, природа которого окончательно не выяснена. Гистерезис может быть уменьшен в 2...3 раза термотренировкой; путем десятикратной выдержки термодатчиков попеременно в жидком азоте (-196 °С) и в нагретом термостате (150 С) в течение часа.

Известно также применение в качестве чувствительных элементов резонансных термометров газовых и жидкостных резонаторов, однако они не вышли за рамки лабораторных образцов [1068]. Апфель в газовом резонансном термометре в качестве чувствительного элемента использовал ампулу длиной 250 мм, заполненную гелием под давлением 2 МПа. Погрешность измерения температуры при 1270 К составила 10 К [1112].

Рис. 10.3. Блок-схема кварцевого термометра [580];

/ - смеситель; 2 - генератор временных импульсов; 3 - схема И , 4 - счетчик; 5 - lUKliponon индикатор; 6 - генератор опорной частоты; Q[, Q[ - чувствительные элементы

Для высоких температур применяются контактные резонансные термометры с чувствительными элементами из тугоплавких материалов [598], Белл предложил использовать в качестве чувствительного элемента термометра четверть- или полуволновой резонатор, соединяющийся со звуко-

Таблица 10.4. Характеристики кварцевых термометров

Параметры

РЦЗ. 382.278ТУ (СССР)

РЦ2. 82Г004ГУ (СССР!

Фирма -Хьюлетт-Паккярд (США)

Диапазон темпера-тур, С

Порог чувствительности, °С

Погрешность градуировки, °С Погрешность стандартной поправки, °С

Дрейф нуля;

за 2 ч

за 24 ч Гистерезис при 100 °С Старение;

за 1 год

за 12 лет Резонансная частота, МГц

Коэффициент термочувствительности, Гц/°С

Нелинейность ТЧХ, °С

Добротность Динамическое сопротивление. Ом Перегрев пьезоэле-мента, °С/мВт;

в воде

в воздухе Постоянная времени тепловой инерции, с;

в воде

в воздухе Габариты, мм, или тип корпуса

-60. + 120 -60 ,+120 -80 ,+250

(0,5 ,2) 10-

(1...5) 10 0,01 ,0,03

(1 ,3) 10 (1 .5) 10-0,001 ,0,01

0,05,.,0,2 0,1..,0,5 5

0,01 при 25 ,200 °С

0,01

0,001..,0,01 0,002..,0,02

5 28 (третий обер-

тон)

170 1000

0,006 (О ,30 °С)

0,07 (О. 100 °С) ,27 (-60 ,+ 120 °С)

(0,1...0,2) Ю (2...3) W 20 40

0,006 0,05 (0... 100 °С) 0,07 0,15 (-40...+250 °С) 0,27 0,7 (при -40 °С)

0,14 0,17

1,2 5...6

4,5Х11Х 13

0,105 0,12

2

018X37

ТО-5

проводом через согласующее звено (трансформатор акустического импеданса) и возбуждать его пакетом колебаний (радиоимпульсом) с изменяющейся частотой заполняющего сигнала (рис. 10.4, в) 1645]. Изменение амплитуды отраженного сигнала при поступлении на резонатор сигнала