Рсзулыаты измерения при внешнем расположении ИПТ существопю улучшаются, если его монтаж производится по схеме, приведенной на рис. 5.6, б. Вытягивая термоэлектроды термопары по поверхности на расстояние / 12/?, получаем расчетную погрепшость измерения, составляющую 5 % максимальной погреилюсти Д оцениваемой по формуле (5.12). Оооснование приводимой оценки и ее уючр.ение с учетом влияния теплообмена рассмотрены в ряде работ 217, 513, 1384]. Так, согласно 11384], разность между действительной температурой / и ее возмущенным на расстоянии г от зоны контакта значением / (г) составляет 5 \ Л оцеиннаемой по формуле (5.12), на расстояниях rlR, примерно равных 5,7; 2,7 и 1,4 соответственпо при ; равном 0,1; 1 н 10 (; = а /?/). ). Формулы (5.12), (5.17) получены для массивных объектов, однако их можно применять при оценке погрешностей измерения, если отношение толщины тела h к размеру ИПТ R, т, е. hiR > 3 при малых значениях разности - t-. Экспериментальные данные о влиянии качества контакта между чувствительным элементом ИПТ и поверхностью тела на точность измерения температуры приведены в работах [64, 112, 249, 324, 513, 1300, 1456].

Необходимое безразмерное время выдержки г (время установления показаний т...) ИПТ от момента его установки на объект с равномерным начальным полем температур находится при alm 3> 1 из уравнения [217, 1341]

э.пер () - в

t у

э.ст

г: {1 - erf (Киг) - ехр [(1 - х) г] erfc г},

(5.22)

т, 2/(э а

8 1/

(5.23)

(5.24)

В формулах (5.22) - (5.24) а, Х, с. у, и Oq, -о, о. То - теплофизические характеристики ИПТ и объекта; 3 .. и (р (т) - температуры чувствительного элемента ИПТ в установившемся состоянии и в момент времени т переходного процесса; erf г = 1 - erfc г - интеграл вероятностей; (э.ст - э (т))/(э.ст - в) < 0,05 при г > 0,11; 0,4; 1,1; 2,3 и 2,7 соответственно для к, равного 100; 10; 1; 0,1 и 0,01.

Погрешность измерения температуры проволок и тонких пластин с помощью термопар при медленном ее изменении или в стационарном режиме теплообмена определяется зависимостью

Д/ = ,-о = -(о-в)

1 + Г1

(5.25)

где <э - измеренная температура в зоне контакта спая термопары с исследуемым объектом (пластина или проволока); <q - действительная температура объекта. Параметр находится по первой из формул (5.13), в которой Лэ, иЛэ2 оцениваются по (5.20) и (5.15); Aq рассчитывается по следук>-щим формулам: для проволоки

До = 2л/? р Y2ao,fi,

где а , Х и R - соответственно коэффициент теплоотдачи, коэффициент теплопрополиос!и и радиус проволоки; для пластины

Ki (у)

/Со (V)

In 1 +

где /Со и Кх

модифицированные функции Бесселя;

(5,27)

(5.28)

*0 о> ho - соответственно коэффициент теплоотдачи, теплопроводность и толщина пластины; Ro - эффективный радиус зоны контакта, определяе-

мый по (5.28) через радиусы термоэлектродов термопары i? и R

Д1етодическая погрешность применяемых на практике ИПТ для измерения температуры поверхности может существенно превышать их инструментальные погрешности и выходить за пределы требуемой точности измерений. При этих условиях ввиду недостаточной надежности расчетной оценки погрешности особую актуальность приобретает разработка методов градуировки термометров, предназначенных для измерения температуры поверхности твердых тел, а также создание соответствующей образцовой и рабочей поверочной аппаратуры. Решению вопросов метрологического обеспечения контактных термоприемпиков, применяемых по схеме

рис. 5.4, а [юсвящена серия работ

425, 988-990].

Вызываемое ИПТ температурное возмущение объекта можно значительно уменьшить, помещая вблизи его чувствительного элемента (например, спаи термопары) миниатюрный электрический нагреватель и с его по-.ющью компенсируя тепловой поток по ИПТ от контролируемого участка поверхности тела. Принципиальные схемы термопар с нагревателями показаны иа рис. 5.7. В варианте I момент компенсации и требуемую мощность электрического нагревателя устанавливают при быстром перемещении термопары вдоль поверхности. Если при смещении спая показания термопары не изменяются, то мощность нагревателя подобрана правильно. В вариантах II и И1 мощность нагревателя изменяют до тех пор, пока сигнал от дифференциальной термопары (выводы 2 к 3 ъ схеме II или выводы 1 и 4 при закороченных выводах 2 и 5 в схеме III) не будет равен нулю. Для термопар расстояние h от поверхности объекта измерения до нагревателя (см. рис. 5.7) колеблется в пределах (1...6) верхности до второго спая равно (0,2... 1)

тродов (0,1...0,4) 10~ м. Применение ИПТ с компенсацией теплоотвода позволяет снизить погрешность измерения температуры неметаллических поверхностей до 0,5...3 К при перегреве этих объектов над средой на 50,..400 К, В течение полувека предложены и исследованы несколько разновидностей ИПТ с компенсацией теплоотвода, их описание дано в работах [284,718,915, 1047, 1135, 1341, 1533, 1544], а также в обзоре [717]. В последних реализациях этого метода использованы электронные компенсирующие устройства [717, 1359, 1529].

Другой метод, описанный в работах [217, 1047], заключается в использовании для измерения температуры поверхности двух ИПТ / и 2, имеющих различные размеры или теплофизические свойства. Их показания i и связаны с действительной температурой поверхности / и температурой окружающей среды соотиошеиием

10 м, а расстояние б от по-10~ м; диаметр термоэлек-

п-в = (э1-в)-

1-а:

э-в ~ в

(5.29)

Входящий в уравнение коэффициент К для цилиндрических термоприем-ннков определяется с учетом (5.13) - (5.15) по формуле

Коэффициент К, слабо злвисяптнй от уровня температуры исследуемого тола, находят по результатам калибровочного опыта при одном известном значении перегрева/ - /в- Расчет иоцтешпостен при раеиоложепни из.ме-рителей по схеме, приведенной на рис. ,5.4, а, значиклыю усложняется для обьектов ограниченных размеров. Ретение некоторых сов.местпых задач

для гермопариых ИПТ дано в 15131.

Для контроля и автоматического регулировапин температуры поверх-

Рис. 5.7. Термопарпые ИПТ с компенсацией теплоотвода: 1,2 - электроды основной термопарк; 3, 4 - электроды вспомогательно!! термопары; 5 - контролируемая повер.хность

Рис. 5.8. Схема установки иепогружаемых ИПТ;

а - бесконтактный способ; 6 - контактный способ; 1 - ИПТ; 2 - теллоизоля-тор; 3 - контролируемый объект

ности промышленных объектов (неподвижных или движущихся) разработана группа так называемых иепогружаемых ИПТ. Упрощенные модели и способы их установки на объект показаны на рис. 5.8. При бесконтактном способе измерения (рис. 5,8, а) ИПТ располагается на небольшом (б = = 0,2...2 мм) фиксироваином расстоянии от объекта. Постоянство прижима при контактном способе (рис. 5.8, б) обеспечивается специальным устройством. Теплоизолятор уменьшает влияние теплоотвода и те\тератур-ное возмущение контролируемого объекта. Принципы проектирования, способы градуировки и оценки методических погрешностей иепогружаемых термоприемников изложены в обзорной работе [954]. Точностные возможности бесконтактных ИПТ, прту\1еняемых для контроля температуры движущихся ленточных материалов, рассмотрены в [326, 327].

5.4. Измерение температуры поверхности массивных объектов ИПТ малой толщины

ИПТ малой толщины конструктивно оформлены в виде пластинок или лленок (обычно прямоугольной формы), длина и ширина которых намного больше нх толщины. Схематически такие ИПТ показаны на рис. 5.9. ИПТ прикрепляют (приклеивают, приваривают, напыляют) на контролируемую поверхность. Поскольку любой пластинчатый ИПТ, как бы тонок он ни был, обладает собственными тепловым сопротивлением и теплоемкостью, его температура будет отличаться от действительной температуры свобод-нон поверхности тела.

Фор.мальный анализ методических погрешностей измерения иестацпо-па1аы\ 1е.\)нерагур может быть сделан иа основе решения двух задач: тен-л>>Т)мсна исс.1едуем()го тела с окружающей средой; теп.тообмена системы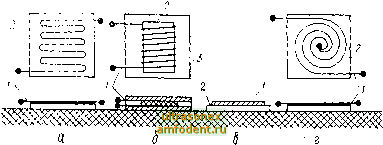

Рис. 5.9. Пластинчатые ИПТ для измерения температуры поверхности: и - проволочный термометр сопротивления, наклеиваем1Л1Т на подложку; б - то же. намотанный на пластинку и закрытый с дву.ч сторон; в - полупровод1.н-ковы1Т термометр сопротивления (болометр), напыленныГ! ил подложку или непосредственно иа исследуемое тело; г - термопара, электроды которой наклеиваются иа п.тастиику или наносятся путем электролитического осалдения; / - чувствительный элемент; 2 - подложка или основа; 3 - защитные пластинки или пленки

ИПТ - тело С той же средой [185 , 208 , 217 , 404 , 621, 758 , 759, 1050, 1289, 1499].

Целесообразно выделить два характерных случая, когда объектом изучения является массивное тело (полупространство) или (пеограниченна я стенка задаиноп толщины (см. 5.5). Учитывая конструктивное оформление ИПТ, распределение температуры в не.м, а также в объекте можно приближенно принять одно.мерным. При этих допущениях получаются относительно простые по структуре аналитические выражения для оценки величины погрешностей [217, 1050].

Пусть массивный объект и система ИПТ - объект (рис. 5.10) подвержены воздействию тепловых потоков удельной плотностью q (т) и 9з (т) или находятся в конвективно-лучистом теплообмене со средой, имеющей температуру t (х). Коэффициенты теплоотдачи и постоянны во времени; начальное распределение температуры в объекте н ИПТ равномерное. Начальная температура принимается равной нулю или выбирается за уровень отсчета температуры. Распределение температур в свободном объекте, а также в системе объект - ИПТ соответственно характеризуется функциями ta [х, т), t (х, т) и 4 (г, х).

Если при наложении ИПТ падающий на поверхность объекта тепловой поток не изменяется (одинаковые терморадиационные характеристики ИПТ и объекта), т. е. q (х) = q (х), то справедливо соотношение [217]

s) = r / (0. S), (5.30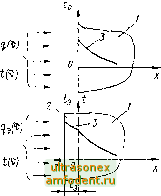

Рис. 5.10. Система плоский ИПТ - массивное тело:

/ - исследуемое тело; 2 - ИПТ; 3 - профили температур

непосрсдствеппо связывающее изображение (г, s) и То (О, s) температуры ИПТ t) (г. т) и лрйсзвительиой температуры f (О, t) поверхности тела. Передаточная функция HN.eeT вид

ch PZ -i- 11 sh рг

chi ;--i-5hp

(5.32)

= I/Jw£ Y£ . (5.33)

г Л.СэУэ

s - параметр преобразования Лапласа; L. - толщина ИПТ, Ь и йэ - коэффициенты тепловой активности обьекта и ИПТ; а,Х, с и у - теплофизические характеристики; индексы О и э относятся соответственно к объекту и ИПТ. Чувствительный элемент может располагаться внутри или на поверхности ИПТ, т. е. координата г или относительная координата Z его размещения принимают в (5.31) различные значения (О < Z < 1) в зависи-мости<Л>т конструктивных особенностей пластинчатого ИПТ.

Если теплоо бмен тела и системы со средой (см. рис. 5.10) осуществляется коивективно-лучистым путем, т. е.

q(T) = a [< (t)-< (0, т)], <?э (г) = аз li(T)-ts (О, т)1, то в.место (5.30) и (5.31) получим [217]

Гэ(г, 5) = К,Го(0, S),

t,a -

ch PZ -f 1] sh PZ

chp + P + И

sh P

(5.34)

(5.35)

(5.36)

Уравнения (5.30), (5.31), (5.35) и (5.36) позволяют анализировать методические погрешности в различных вариантах измерения температуры поверхности с разной степенью приближения расчетных зависимостей.

Ограничиваясь в разложении передаточной функции членами разложения не выше второго порядка, из (5.31) получаем

l+ri2p+-22p2

+ 1-

+ -(l-Ti2Z)p + B p2

l--i-(l-r,Z)p-f Во Р-

(5.37)

Используя (5.37) и (5 30) и переходя к оригиналам, находим следующие приближ енные соотношения, определяющие методическую погрешность измерения температуры поверхности А( (г, т) в зависимости от действительной to (О, т) или измеренной t (г, т) температуры;

Д/ (2, т) = (г, т) - to (О, т) ;

(\fZ- - 1)L {Ks7 y(0, .)) -1-

(.5.38)

ГЛР символ /,

означает операцию обрат ного преобра.зчсь! мл Jiaii.iaca иы-

р.ыллшч ! Т, (г, s) НЛП fsTg (О, i);

\. = --2 + i-(Z-i).

(5.39)

Первым из уравнений (5.38) нредпоччтмьно поль.)оваться при т) < I вторым - при 11 > 1.

Если температура (z, г) или /о (О, т) изменяется, в частности, с течением времени по степенному закону вида

t-, (г, X) = Ах или 0 Ф, X) = Ах при m > О, то нз уравнений (5.38) после преобразований получае.м

Д, (г, X) = I, (г, т) - if, (О, т)

(5.40)

1( г-1)С(.)-М

ч 1л)э

(г, т) Fo

±(,.z ,)C(.,Al-i-.. .A

(5.41)

где С (т) - некоторое число, определяе.\юе чере.з гам\1а-4)упкцп!; Fo., - безразмерное вре.мя (число Фурье), отсчитываемое от начала процесса (х =

С (т) =

Г (т 4-

Г т + .

Fo, =

При m = 0; 1/2; I и п (п - целое число) Гп 2

С (т) = - ;

Гп !

(5.42)

(5.43)

2 ] л 1 3 . 5. . . (2п- 1) Г л Из (5.41) следует, что если воздействие теплового потока q (х) приводит к монотонному увеличению измеренной температуры 4 (г, х) по закону (5.40), то относительная погрешность измерения температуры поверхности Д/ (г, г)э (г, х) будет постепенно уменьшаться по мере увеличения критерия Fog. Требуемое время х, начиная с которого относите льная погрешность измерения температуры поверхности ие превысит заданной, находят непосредственно из (5.4 1).

В зависимости от свойств ИПТ и объекта (отношение тепловых активностей )1) и расположения чувствительного элемента (значение координаты ) методическая погрешность Д( (2, х) может быть как положительной, так и отрицательной, т. е. измеренная температура (г, х) может опережать действительную температуру поверхности (О, х) или отставать от нее. В частном случае, при расположении чувствительного элемента, удовлет-