лучения, полученное Планком, и фундаментальное уравнепне Найквиста, связывающее основные параметры шумовых явлений. Эти результаты наряду с идеальным газовым термометром могли служить основой для абсолютной термодинамической температурной шкалы. Последуюн1ее развитие вероятностно-статистического метода привело к возникновению понятии о неравновесных и отрицательных абсолютных температурах.

Температура является интенсивным параметром. Остальные шесть основных метрологических параметров - длина, масса, время, сила света, количество электричества, количество вещества - по своей природе экстенсивны и обладают свойством суперпозиции. Сложение и деление основных единиц например килограмма, обеспечивает надежную метрологическую основу измерения массы при произвольно больших и малых значениях измеряемой величины. Температура таким свойством суперпозиции не обладает, и это всегда вносило большие трудности в проведении измерений.

Для практических целен наряду с теоретической термодинамической температурной шкалой вводились шкалы, связанные с определенной системой реперных точек и средств реализации интерполяции. В 1889 г. Пер-, вая международная конференция по мерам и весам утвердила Нормальную водородную шкалу . Последующие коррективы в редакции температурных шкал вносились после тщательной предварительной подготовки на международных официальных собраниях в 1927 г., 1948 г. и 1968 г. В настоящее время действует Международная практическая температурная шкала (1968 г.), сокращенно обозначаемая МПТШ-68.

В широком диаЛзоне измерений газовый термометр длительное время являлся единственным средством передачи термодинамической температурной шкалы. О сложности работы с ним можно судить по тому, что этот инструмент требует кондиционируемого помещения площадью в несколько десятков квадратных метров. Это обстоятельство привело к тому, что передача шкалы охвачена сложной системой реперных точек и средств интерполяционной передачи в виде термометров сопротивления и термопар. Естественный для метрологов консерватизм стал тормозом дальнейшего развития. Какими же могут быть ожидаемые пути развития метрологии?

До настоящего времени только три фундаментальных явления могут быть положены в основу передачи. Они выражены уравнениями Клапей.о-на. Планка и Найквиста. Значительное повышение культуры теплометри-ческих и частотно-спектральных измерений с помощью новой аппаратуры открывает возможности перераспределения диапазонов передачи шкалы. На основании закона Стефана - Больцмана (частный случай закона Планка) можно провести надежную передачу с погрешностью, несущественно превышающей 10 измеряемой величины абсолютной температуры, начиная с 200 К и выше, без ограничения.

Появление аппаратуры частотно-шумового анализа с высоким разрешением позволит создать чувствительные элементы, по размерам несколько превышающие таковые у термометров сопротивления и термопар, непосредственно передающие термодинамическую температурную шкалу в каждом Производимом измерении. При этом отпадает надобность в Международной практической температурной шкзде с ее системой реперных точек. Бесконтактная термометрия сможет опираться на закон Планка, в частности на уравнение Стефана - Больцмана, контактная - на уравнение Найквиста.

Значительное улучшение условий международного сотрудничества метрологических организаций наиболее развитых стран мира привело к тому, что в течение.,последних 10 лет существующая МПТШ-68 подверглась обоснованной всесторонней критике. В связи с этим вскоре должна быть опубликована радикально переработанная Международная практическая температурная шкала, которая и явится метрологической основой всех температурных измерений.

ГЛАВА 2

ФИЗИЧЕСКИЕ ОСНОВЫ ТЕМПЕРАТУРНЫХ ИЗМЕРЕНИЙ

2.1. Температурные шкалы

Температура, относящаяся к категории интенсивных физических величин, требует для своего измерения наличия не только единицы, но и шкалы, по которой отсчитывается значение измеряемого уровня. Единица измерения определяет масштаб шкалы.

Температура не поддается прямому измерению, и всякий прибор, предназначенный для ее измерения, преобразует температуру в другую, легко измеряемую физическую величину, используя однозначную связь с температурой выбранного физического (термометрического) свойства вещества.

Под термином температурная шкала принято понимать непрерывную совокупность чисел, линейно связанных с числовыми значениями какого-либо удобно и достаточно точно измеряемого физического свойства, представляющего собой однозначную и монотонную функцию температуры. Принцип построения температурной шкалы заключается в том, что выбирают какие-либо две основные (или опорные) точки, представляющие собой легко воспроизводимые температуры, неизменность которых может быть обоснована общими физическими соображениями, например температуры кипения или затвердевания чистых веществ. Этим температурам приписывают произвольные числовые значения и Температурный диапазон t. - ti часто называют основным диапазоном температурной шкалы. Его делят на некоторое целое число N равных частей и 1 V часть принимают за единицу измерения температуры или за масштаб шкалы, экстраполируемой в одну или обе стороны от основного диапазона.

Далее выбирают термометрическое свойство Е. (В качестве термометрического свойства в начальную эпоху развития термометрии использовалось объемное тепловое расширение жидкости в твердой оболочке.) Это свойство условно принимают линейно связанным с температурой, т. е. полагают справедливым равенство

di = kdE, (2.1)

где k - коэффициент пропорциональности. Интегрирование (2.1) дает

( = kE + C. (2.2)

Для определения постоянных k-a С используют две выбранные выше температуры ti и t, для которых экспериментально находят соответствующие значения и Е. Тогда вместо (2.2) будем иметь

t=k+ (Е-Е,). (2.3)

Последнее выражение получило название уравнения шкалы. С помощью уравнения (при условии, что допущение о справедливости (2.1) остается правомерным) но измеренному значению/; рассчитывается само значение температуры t.

Исследования показывают, что в природе не существует физических свойств, связанных линейно с температурой. Коэффициент k в (2.1) для любого термометрического свойства сам является функцией температуры, причем для разных свойств вид этой функциональной зависимости различен. Из этого следует, что описанным методом можно построить столько шкал, сколько выбрано термометрических свойств. Совпадая в основных точках ti и 2, эти шкалы давали расход5пцисся значения температур как внутри диапазона ti - t, так и вне его.

2.2. Термодинамическая температура

Недостатки эмпирических шкал заставили отказаться от использования конкретных термометрических свойств и искать способ построения шкалы, независимой от свойств конкретных веществ. Решение задачи было найдено на основе свойств идеальной тепловой машины, работающей по

циклу Карно.

Цикл Карно описывает изменение состояния определенной массы газа, заключенного в цилиндре с поршнем. Цилиндр окружен тепловой изоляцией и может приводиться в тепловой контакт с нагревателем с температурой Г, и холодильником с температурой Т. Изменение состояния газа в процессе цикла схематично представлено на диаграмме (рис. 2.1). Начальное состояние газа, например в точке А, характеризуется значениями Р К 7, его параметров. С помощью поршня создается адиабатическое (без теплообмена с внешней средой) расширение газа, за счет чего температура снижается до значения Т. Объем газа принимает значение (точка В на диаграмме). Газ приводится в контакт с холодильником, температура которого Т, медленно сжимается поршнем, причем выделяющаяся при сжатии теплота передается холодильнику. Изотермический при температуре Т2 процесс сжатия продолжается, пока объем газа не достигнет значения Уз (точка С на диаграмме). В этот момент холодильник отключается, и при дальнейшем адиабатическом сжатии газа его температура повышается до значения Т. Объем газа принимает значение (точка D на диаграмме). Здесь подключается нагреватель и газ изотермически расширяется с температурой Ti до возврата в точку А диаграммы. Об-Ьем газа принимает исходное значение Vi. Цикл завершен.

Коэффициент полезного действия (КПД) такой идеальной тепловой машины определяется выражением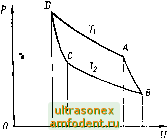

и, U2

Рис. 2.1. Изменения состояния газа в процессе реализации цикла Карно.

(2.4)

где Qi - количество теплоты, отданное нагревателем рабочему телу (газу), Q2 - количество теплоты, отданное рабочим телом холодильнику. Так как цикл Карно построен на законах термодинамики, то и температура, входящая в выражение (2.4), получила название термодинамической.

Согласно (2.4) КПД идеальной тепловой машины определяется только значениями температур ее нагревателя и холодильника 7 и не зависит от направления прохождения цикла, а также, что самое важное, ие зависит от свойств рабочего тела. Это свойство КПД цикла Карно в середине ХГХ в.

навело на мысль об использовании законов термодинамики для осуществления эталонной шкалы температур.

Можно показать, что температура, входящая в уравнение Клапейрона состояния идеального газа

PV := RT, (2.5)

является также термодинамической. В законе и]арля

Р< = Ро(1+7). (2-6)

определяющем изменение давления идеального газа (при постоянном объеме), термод1п1амнческая температура t отсчитывастся от некоторого уровня Tfs- .Аналогичная по форме связь устанавливается для изменения объема идеального газа при постоянном давлении законом Гей-Люссака:

(2.7)

Физический смысл коэффициента у в (2.6) н (2.7) становится ясным из следующих соображений. По мере понижения температуры Удавление газа pt согласно (2.6) убывает. Можно определить такое значение о, при котором pt = 0. Из (2.6) очевидно, что = -1/у. Температуру принято называть абсолютным нулем температур. Так как значения < отсчитывались от некоторого уровня Гд термодинамической температуры, то = 1/у.

Для реальных газов (2.6) и (2.7) принимают вид

Pi Ро (1 -г а 0, = Уо (1 + V).

(2.6) (2.7)

где а , и зависят как от давления газа, так и от его температуры. По мере снижения давления свойства реальных газов приближаются к свойствам идеальных и lim a.-j - lim Хр -= у.

2.3. Газовые термометры

Реализация идеального цикла Карно встречает непреодолимые трудности Поэтому для построения практической температурной шкалы целесообразно использовать физические законы, в которые входит термодинамическая температура в качестве основного аргумента, например уравнение Клапейрона (2.5).

Созданные для этой цели приборы, в которых в качестве рабочего тела используется определенный газ, получили название газовых термометров. В зависимости от использованного принципа газовые термометры создают либо с постоянным объемом рабочего резервуара, либо постоянного давления. В пе,-)вом случае в зависимости от изменения температуры меняется давление газа (уравнение (2.6)), а во.втором - его объем (уравнение (2.7)). Более точные результаты удается получить с газовым термометром постоянного объема.

Принципиальная схема газового термометра представлена на рис. 2.2. Рабочий резервуар /, изготовленный из материала, устойчивого в том диапазоне температур, на который рассчитан термометр, заполняется рабочим газом. Тонким капилляром 2 резервуар соединен с пространством над поверхностью ртути в коротком колене 5 манометра. С помощью специального устройства, либо визуального, либо емкостного, ртуть в коротком колене перед отсчетом устанавливается под пробкой с одним и тем же зазором, что обеспечивает постоянство объема рабочего газа. Давление рабочего газа определяется по высоте мениска столба ртути в длинном колене

манометра 5, отсчитываемой по шкале 4. Уровень ртути в коротком колене манометра устанавливается с помощью поршенька 7 и вспомогательного резервуара 8. Система заполняется рабочим газом через трубку 6 после п[)едвартельного опускания ртути в длинном и коротком коленах.

Для низких температур удобно бы.ю применять рабочий резервуар из красной меди, обеспечипаюнГин вмрпвнивание температур во bicm обт>еме газа. Для средних TCNUieptnyp применялись стеклянные резервуары, а для высоких - резервуары из сплавов плгггипы и иридия или платины и родия, обеспечивающие .хорошую i а-.онспроиинаемость до техшературы свьнпе 1100 °С. Для высоких к-мнератур нснользовался также резервуар и.з литого кварца.

Очевидно, что тепловое расширение материала резервуара в шнроко.ч диапазоне температур приводит к -нзыеиению рабочего объема газа. Поэтому для внесения соответствующих поправок либо сам резервуар, либо образец, изготовленный из того же материала, что и резервуар, подвергают специальному исследованию с целью установления возможно более точной формулы, определяющей зависимость изменения коэффициента его линейного расширения от температуры.

Выбор рабочего газа также определяется той областью температур, для измерения в которой предназначен термометр. Для низких TeNmepaTyp в качестве рабочего газа принимается гелий, позволяющий нижний предел измеряемых температур снизить до 10 К, а для высоких - азот, менее, чем гелий, диффундирующий при высоких телше-ратурах через стенки резервуара.

-1спользование реальных газов приводит к необходимости введения поправок к показаниям газового термометра для приведения их к термодинамическим температурам. Эти поправки находятся расчетным путем на основании заранее тщательно проведенных исследований отклонений свойств данного газа от законов идеального газа.

Таким образом, газовый термометр является тщ инструментом, с помощью которого может практически измеряться термодинамическая температура.

Кроме указанных выше в показания газового термометра необходимо вводить еще целый ряд других поправок. К ним относится поправка на величину вредного объема термометра, состоящего из объема капилляра и объема, заключенного в коротком колене манометра между мениском ртути и пробкой; поправка на температуру газа в отдельных частях этого вредного объема; поправка на температуру ртути в коротком и длинном коленах манометра; поправка на температуру шкалы отсчета и др.

Для получения необходимой точности измерения термодинамических температур проведение газотермических измерений требует тщательного учета влияния многих факторов и может быть надлежащим образом выполнено только в крупных метрологических лабораториях.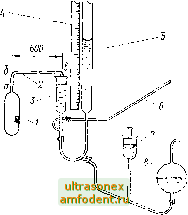

Рис. 2.2. Принципиальная схема газового терлюметра:

/ - рабочие резервуар; 2 - капилляр; 3 - короткое колено манометра; 4 - шкала; 5 - длинное колено манометра; 6 - трубка для заполнения системы ртутью; 7 - поршень; 8 - ре зервуар с ртутью

2.4. Термодинамическая температурная шкапа

Термодинамическая температурная шкала, осуществляемая с по.мощью газовых термометров, базировалась на двух (реперных) точках: температуре равновесия между льдом и водой (точка таяния льда) и температуре равновесия между водой и ее паром при нормалг.иом атмос([)ерном давлении (ючка кипения воды). Первой точке условн1 приписывалась цифра О, а второй - цифра 100. Диапазон температур между этими основными точка-\\и делился на 100 равных частей и сотая его часть получила название градуса как единицы измерения термодинамической температуры или масштаба термодинамической температурной шкалы.

Из (2.5) при V = const непосредственно вытекает, что

100 Tq

а для любых температур Т

(2.8)

В 1927 г. на VII Генеральной конференции по мерам и весам принято решение о том, что все измерения температур во всем мире должны в конечном счете приводиться к термодинамической температурной шкале.

При этом числовые значения температур, отсчитываемые от Т (точки таяния льда), обозначались через / и сопровождались знаком °С (градус Цельсия), а отсчитываемые от абсолютного нуля - через Т и сопровождались знаком °К (градус Кельвина). Для То принято значение 273,15 (точно). Поэтому было установлено соотношение

Г (К) =П°C] + 73,I5.

(2.9)

Физические ограничения и технические трудности приводят к тому, что осуществление термодинамической температурной шкалы с помощью газового термометра ограничено для низких температур значением 10 К, а для высоких температур значением 1100 °С. При более высоких температурах заметно проявляется диффузия рабочего газа через стенки резервуара.

Исследования в дальнейшем показали, что воспроизводимость основных точек шкалы - точки таяния льда и точки кипения воды - не может быть достигнута лучше 0,001 К, и это обстоятельство накладывает ограничения на дальнейшее повышение точности измерения термодинамических температур. Поэтому в 1968 г. было принято новое определение единицы температуры, названной Кельвином (К). Кельвин определяется как 1/273,16 термодинамической температуры тройной точки воды. Тройная точка воды представляет собой температуру равновесия трех фаз - твердой, жидкой и газообразной - чистой воды естественного изотопного состава. Она принята равной 0,01 °С, т. е. на 0,01 К выше точки таяния льда, которая теперь исключена из числа основных.

Таким образом, новое определение единицы темьературы предусматривает использование только одной практически реализуемой реперной точки. Вторая необходимая репериая точка - теоретическая - абсолютный нуль.

Воспроизводимость тщательно подготовленной тройной точки воды составляет ~ 0,0002 К. Лучшая воспроизводимость тройной точки воды по сравнению с точкой таяния льда и отсутствие влияния погрешностей при воспроизведении второй основной точки привели к более точному установлению единицы температуры по новому ее определению.

Символ К употребляется при числовых значениях температур, отсчитанных от абсолютного нуля, разностей температур и в формулах размер-