

 |
 |
|
Главная страница Магинтогидродинамическое измерение температуры 1 i- \i <f 2 (b + /I) 1 - 46/1 3 температура НПТ (пзмерсииая температура); ti - диаметр 1ЬГГ. Если температура поверхности объекта 1 {%) нестациопариа, то дтш-мическая составляюитая Ад (т) погрешности измерений приблпжетю определяется но формуле dt, (т) А , (X) = /э (X) - (т) = (ео - бэ) 4 I , СзУ: / 6А - 2{b + h) + nd (5.68) (5.69) en = (b + A)2 c v 8я2Х a через с и у с соответствующим индексом О , э и з обозначены удельная теплоемкость и плотность материала тела, ИПТ, замазки. При практической реализации данного способа измерений желательно, чтобы глубина и ширина паза не превышала 0,2...0,8 мм. Замазка выбирается с относительно высокой теплопроводностью. Чувствительный элемент по возможности чекаинтся или приваривает( я к исследуемой по-, BtpxHOCTH. Для непрозрачных объектов с высокой степепью черноты по- верхпости погрешность измерения прн Я > Яд грубо оценивается по соотношению < (5.70) в котором сохраняются прежние обозначения. Следует с осторожностью относиться к покрытию места расположения спая металлической фольгой, бумагой и т. п. В некоторых случаях из-за разницы в коэффициентах излучения и поглощения покрытия и поверхности тела при наличии внешних источников теплового излучения роль покрытия может оказаться отрицательной. Выход чувствительного элемента ИПТ на поверхность тела. Неискаженные влиянием ИПТ условия теплообмена тела со средой подчиняются соотношениям (5.65). Приближенная оценка методической статической погрешности измерения температуры поверхности тела для данного случая выполняется по уравнению 217) 1 - At = t-tu- (э-в) = (in -to), (5.71) P = /il; (5.72) 4 и - измеренная и действительная температуры поверхности; d - диаметр ИПТ; Аз и Яз - толщина и теплопроводность зазора (замазки, воздуха, контактного слоя), отделяющего lillT от объекта (рис. 5.14). Влияние конструктивных и теплофизических факторов выявляется непосредственно при анализе соотношения (5.71). Помимо [2171 различные варианты расчета и экспериментальное исследование этого случая измерений рассмотрены также в работах [955, 1000, 1050. Пусть ИПТ (термопара, спай которой выходит иа поверхность) применяется для регистрации кратковременных (импульсных) тепловых процес- 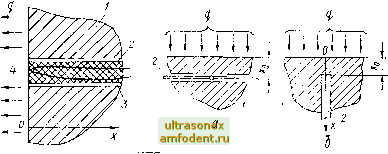 Рис. 5.14. Рас1юложепие mil в толще тела с выходо.м чувствительного элемента на поверхность: / - исследуемое тело; 2 - ПТ; 3 - зазор, 4 - среда Рис. 5.15. Расположение ИПТ внутри тела: а - в канале; б - в толще тела; / - исследуемое тело; 2 - ИПТ СОВ. Тогда взаимосвязь измеренной 3 (х) и действительной t (х) температур в предположении, что объект и термопара практически не взаимодействуют между собой (Хз = 0) и ведут себя как полупространство, определя.ется выражением з(х)=А, ,т)= /.1 (х), (5.73) где 6q и 63 - тепловые активности; X, с и у - соответствующие теплофизические характеристики тела и ИПТ. Входным тепловым воздействием при выводе формулы (5.73) являлся тепловой поток q (х), одинаковый для термопары и тела. Картина теплообмена усложняется, если тепловое воздействие происходит конвективно-лучистым путем от среды с температурой t (х). В этом случае выполняется следующее соотношение: Уз is) То is) (5.74) о b.fs где а - коэффициент теплоотдачи. При монотонном процессе нагрева с течением времени х роль слагаемых а,/6о К и уменьшается и из (5.74) получается выражение, одиогииное формуле (5.73). CooTHOiuemii, (5.73) и (5.74) справедливы, если в начальный момент Гфемени (0) = п (0) = 0. Расположение ИПТ в глубине тела без выхода на поверхность. Bo3mo?i.\-ны два характерных случая размещения, условно показанные иа рнс. 5.15. При расположении по схеме, показанной на рис. 5.15, а, ИПТ (обычно термопара) вытянут вдоль изотермической поверхности и расположен в канале, удаленном от поверхности иа рассюяпие х . Пусть ППТ достаючио .миниатюрен и находится в центре канала. Тогда прибли:;;е;п1.. с учетам oipa-ииченин, изложенных в гл. 4, можно полагать, что в сгацис.чьчриом режиме теплообмена средняя температура его чувствительного э.ц-.меита /, cooibct-ствуот температуре t (хо) в занимаемой ИПТ области. В результате измерений необходимо внести поправку, учитывающую градиент техтератур по глубине. При одномерном тепловом потоке через плоскую или цилиндрическую поверхность формулы для поправок получаются из общеизвестных уравнений стационарного распределения температур [217, 1050] (5.75) Д/ = <э - = - 2яХ 2я?. где t - действительная температура поверхности тела (х = 0); q - удельный тепловой поток в расчете на единицу площади плоской поверхности или единицу длины цилиндрической поверхности; Ig - теплопроводность тела; Гд ч - соответственно внешний радиус цилиндрического тела и радиус расположения чувствительного элемента термоприемника (г - - /-д = л-о). В нестационарном режиме теплообмена пересчет показании \шниатюр-ного ИПТ, удаленного от поверхности на расстояние Хд и не искажающего поле температур в исследуемом теле (см. рис. 5.15, а), осуществляется согласно уравнению / V. 7-. (S) Тп is) ехр и /- (5.76) Здесь входным воздействием является тепловой поток q (т), а 7э ( ) и {$) - изображения измеренной (т) и действительной (т) температур поверхности. После обратного преобразования имеем 2 VmJ V(t:- 4а (т - ц) 1д(т-ц)ац, (5.77) где т) - переменная интегрирования. В частных случаях предпочтительнее вместо (5.77) пользоваться выражением (5,76), подставляя в пего Тс, {$) или Tj, (s), найденные по известным или предполагаемым зависимостям 4 (т) или t (т). -Амплитудно- и фазочастотные характеристики определяются по (5.76) или непосредственно из решений о прохождении температурных воли в полупространстве: AiQ) = Q(0) ф (Q) = - Q, где Q - безразмерная частота колебаний: (5.78) (5.79)  а (0) и я (лго) - амплитуды колебаний действительной (т) н измеренной 4 (т) температур тела, Г и со - период и частота колебаний Простое аналитическое решение для оценки погрешности измерения при расположении ИПТ по схеме рис. 5.15, б ие найдено. Температурная погрешность и ее знак зависят от соотношения между теплофизическими свойствами ИПТ и объекта, диаметра ИПТ, глубины д- его залегания, а также от характера теплового воздействия на поверхность. Результаты исследования для крайних случаев 1. > Хд или Kg > изложены в статьях [68, 1140, 1438[, Числовые примеры оценки погрешностей по формулам (5.6) даны в [217]. 5.7. Пространственно-временное восстановление температуры по ограниченному числу результатов измерений В практике температурных измерений известна группа задач, решение которых традиционными средствами измерений сопряжено со значительными трудностями, так как подлежащая контролю температура в выбранной точке объекта выходит за пределы допускаемого температурного интервала работы ИПТ. Такие экстраполяционные задачи актуальны в металлургии, газовой динамике, плазменной технике. Несмотря на сравнительно большое количество патентов и авторских свидетельств, практический их выход остается достаточно скромным, что объясняется несколькимп причинами: сложностью моделирования физической картины процессов, недостаточной проработкой методических основ и ограниченным опытом, накопленным в этой области [1048[. Значительная часть работ направлена на решение задачи определения стационарной температуры жидких или газовых сред. Сущность применяемых методов, часто называемых динамическими, состоит в испол1>:човаиин начального участка переходного процесса (кривых разогрева) одного или нескольких ИПТ Последующая обработка соответствующих кривых (ручная или автоматическая) позволяет рассчитать стационарную температуру среды, принимаемую за действительную. Различные приемы обработки исходных данных переходного процесса рассмотрены в работах [207, 208, 217[. Выделяются методы, основанные на периодическом кратковременном погружении измерителя в исследуемую среду и анализе квазистационарной температуры при различных частотах погружения [820, 11581. Оценка методических погрешностей восстановления температуры зависит от выбранных условий обработки кривых переходного процесса. Исследование некоторых модификаций динамических методов показывает, что их точность на существующем уровне реализации оказывается недостаточной. Одна из причин состоит в том, что экстраполяционные формулы, полученные при использовании линейной теории теплопроводности, распространяются на температуры, значительно отличающиеся от регистрируемых значений. Температурная зависимость теплофизических свойств измерителя и среды, а также действие лучистого, теплообмена приводят, как показано в работе [882], к систематической погрешности, достигающей 20 % и более для температур 3000...5000 К. Число экспериментальных работ ограничено [82, 820]. В последнее время интенсивно развиваются методы восстановления температурных полей в объектах по ограниченному числу точек измерений, основанные на закономерностях теплопередачи внутри исследуемого объекта. Помимо самостоятельного интереса - определения поля температур и их локальных значений в труднодоступных местах объекта - эти методы помогают в решении иных целевых задач. К таким задачам относятся, например, определение условий теплообмена на границе объекта и среды, т. е. нахождение температуры и теплового потока на границе, определение коэффициента теплоотдачи или температуры среды, окружающей объект. Самостоятельное иаправленнр представляют задачи нахождения теплофизических или других температурно-зависимых характеристик объекта. Общей теоретической основой методов восстановления температурных полей и связанных с ними исследований тепловых процессов являются аналитические или машинные (численные) решения обратных задач нестационарной теплопроводности (1300]. В зависимости от конкретной направленности и строгости постановки определяемых прикладными целями исследований приемы и алгоритмы решения обратных задач широко варьируются. Методические погрешпостн восстанавливаемых температур и базирующихся на и.х основе других теплообмеиных н теплофизических характеристик преимущественно оцениваются исходя из частных особенностей рещае\юй задачи. Систематизированные сведения и методика оценок погрешностей различных теплофизических величин представлены в [17, 217, 457, 458, 463, 465, 626, 747, 753, 871, 876, 1031), где приведена подробная библиография. 5.8. Измерение температуры поверхности полупрозрачных объектов плоскими ИПТ В услиях воздействия теплового излучения появляется дополнительный по сравнению с непрозрачными телами источник методической погрешности - искажение теплового действия излучения в окрестности установки ИПТ, вызванное различием радиационных свойств ИПТ и объекта, а также объемным характером поглощения излучения в объекте. На рис. 5.16 представлена схема измерения температуры поверхности полупрозрачного объекта плоским круговым ИПТ, чувствительный элемент которого нанесен на подложку. Анализ задачи приводит к следующей зависимости для погрешности измерения [300, 1051]: А = и, - Un = Ада + А/ + 2 \j, (/ = О, V, S). (5.80) Здесь - измеренное (температура чувствительного элемента ИПТ) и Un - действительное значения температуры тела; Аог, - погрешность от перегрева ИПТ измерительным током уделбной- мощностью а э, Вт/м; А - погрешность из-за отличия внешиего теплообмена свободного объекта и системы объект - ИПТ со средой; А у - погрешность из-за разницы потоков излучения, поглощенных ИПТ и объектом. Предполагается, что спектральная зависимость падающего потока излучения и радиационных свойств полупрозрачного объекта учитывается использованием спектрозональных значений характеристик я пределах спектральных областей прозрачности, объемного и поверхностного поглощения излучения. Поэтому плотность потока излучения q, Вт/м, падающего на объект, равна сумме потоков q, Qy и q, соответствующих трем спектральным областям, т. е. = 2 qj, где / = 0; V, S. 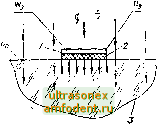 Рис. 5.16. Схема тепловых воздействий при измерении температуры поверхностипо-лупрозрачного тела: / - чувствительный элемент ИПТ, 2 - подложка (контактная прослойка), 3 - объект. Структура составляющих методических погрешностей Д раскрывается соотношениями в которых обозначено yf,f{t - Ui), 1 == э, п, г = э, п \ \ / - О, !-, S I к -1- А-, - /. (5.81) (5.82) У 4.0.1 = У,: = У g.SJ = y.v.i = + 1 (5.83) Индекс i означает, что известна либо действительная температура поверхности п, либо измеренная температура и,. В выра>вения (5.83) входят следующие коэффициенты: П = i + * + Э. = I + !о, *п = - , /г, = - (5.84) Комплексы Пп Q - --- v.v = . £k 1 + 0,44 \%), (5.85) характеризуют интенсивность теплообмена: с окружающей средой на поверхности объекта и ИПТ -д, Jg; в области объекта г возмущенным температурным полем - £; через подложку ИПТ и контактный слой - 1. В формулах (5.81) - (5.85) обозначено: R - эффективный радиус, - поверхность контакта с объектом, - Геплоотдающая поверхность, - поверхность, воспринимающая поток излучения, Уэ - объем чувствительного элемента ИПТ; ао - суммарный коэффициент теплообмена объекта с окружающей средой; а, - коэффициент теплопередачи между чувствительным элементом ИПТ и окружающей средой; к - коэффициент теплопередачи через подложку и контактный слой; а - ) г 3 t теплопроводность объекта; Лцд, Ау - p c, 5.17. График функции / (х). 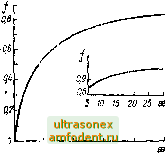
|
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |