воряюшеп) требованию ZIll первые слагаемые уравпсппи (0.,3 ) и (5.41) обращаются в пуль, и дш.амитеская погрешность приближенно one-иивается юлько вторыми слагаемыми этих уравиеинИ.

Если теплообмен объекта определяется воздействием температурь! середы t (т), то для оценки ногреш[остен используют выражения (5.,35), (5.3b). Приближеппо

1 +Т1(1 -2)р-гЬ.#

1-т(1-г)Р-Д #- (5.44)

Подставляя выражение (5.44) в (5.35), иаходнм искомые ypaniieumi взаимосвязи ногрещпости Д, (г, т) с измеренной /, (г, т) или деистпительпон t (О, X) температурами:

Д/ (2, т) = /э

г, т) - h, (О, т) dt, (г, X)

- б,

K,} (Z - 1) L-,у, dt (О, X)

[fsT, (О, S))-

(5.45)

бэ.а =

(1 -Z-i)-112(1 -Z)-

(i-n).

t4 i

Z) - (1 -Z)-r -(1

(5.46)

Первое из выражений (5.45) обеспечивает более высокую точность оценок при т) < 1 и Z 1, а второе - соответственно при )) > 1 н Z 0.

Если температуры 1-, (г, т) или (О, х) изменяются по закону (5.40), то из выражений (5.45) получаем

Д (г, т) = /э (г, X) - ig (О, х)

il(Z- l)C(m)

71 (Z- l)C(m) to (0, t:

/э (г, т)

в и, Т)

/РОз

- mfl

<о(0. г) Fo,

(5.47)

В уравнениях (5.47) С (т) и Fog определяют по (5.42) и (5.43), а коэффициент Кэ - по (5.32). Из (5.45) и (5.47) следует, что при Z = 1, т. е, при расположении чувствительного элемента на стороне нагрева, первая составляющая погрешности, пропорциональная L~ {VsT- (г, ,s)} н

[VsTf, (О, s)}, исчезает, и погрешность измерения будет линейной функцией скорости изменен-ця во времени температур <э (г, х) и tg (О, х).

Если воздействие на объект теплового потока q (т) или температуры среды t (т) периодически изменяется во времени, то это приводит к периодическому в квазиустановившемся режиме изменению температуры поверхности объекта /о (0. т) и показаний ИПТ (г, т). Для оценки динамики процесса измерений используют амплитудные и фазовые частотные характеристики, получаемые на основе выражений (5.31) и (5.36). Ограничиваясь в разложении передаточной функции (5.31) слагаемыми степени не выше s, находим

(5.48)

-= A,>iZ, Ay =

-4, =

(1 -z) Ki

л - 2

Заменяя в (5.48) .s на ш, после преобразований получаем

А (м) -d = / \+У2В,УЪ+ B]is,

1 ~/24i (I + Л.,ш) + -4[ш + -4-;u)2

(р (w) arctg

j7g (-4,-51 + 514,0,)]+ ,4.до

(5.49)

(5.50)

(5.51)

Уравнение (5.50) опреде.дяет амплитудно-частотную характеристику системы ИПТ - объект, показывающую отношение акшлитуды ,4, колебаний температуры /, (2, х) чувствительного элемента ИПТ к амплитуде At изменения температуры (О, т) поверхности объекта в зависимости от циклической частоты ш. Фазочастотиая характеристика (5.51) определяет сдвиг колебании те\шературы ИПТ по отношению к температуре тела.

Если исходным тепловым воздействием на объект является температура среды t (т), то выражение (5.36) для Y, можно при любых т) и iZ < 2 приблидчсиио представить в виде, аналогичном (5.48). Для этого случая ам-плнтудио- и ([азочастотпые характеристики рассчитывают по уравнениям (5.50), (5.51), в которых коэффициенты В Л, и определяются по форму-

В, = ;Сэг)(г + -1), л, = /(зт) (l + 2= Kl\-(\-7J)-\-~(\-цЧ)

(5.52)

Числовые примеры оценки методических погрешностей приведены в [217, 1050]. Соотношения (5.37) - (5.51) представляют собой первые приближения решаемой задачи, определяющие методическую погрешность при относительно медленных изменениях температуры во времени и в моменты времени, далекие от начального. Учет высокоскоростных (высокочастотных) составляющих погрешности следует проводить, пользуясь более стро-гшш аппрокси.мациями передаточных функций (5.31) и (5.36).

5.5. Измерение температуры поверхности стенок плоскими (пластинчатыми) ИПТ

Погрешность измерения стационарибй температуры стенки. Пусть стенка (рис. 5.11, а), имеющая толщину L и теплопроводность Xq, разделяет две среды с постоянными температурами и t. Коэффициенты конвективно-лучистой теплоотдачи между средами и поверхностями стенки равны otj и а.,. Измерению подлежат действительные температуры поверхностей стенок, обозначенные f j и 2- качестве ИПТ применяются плоские ПТ толщиной /.а, имеющие теплопроводность к и закрепленные соответственно на левой (рис. 5.11, б) или правой (рис. 5.11, в) поверхностях стенки. Чувствительный элемент ИПТ размещается в плоскости ПТ с координатой г, причем О < 2 1. Показания ИПТ 4 (г) будут отличаться от

искомых температур поверхностей стспки /. , и 1 , поскольку ИП[. обла-д.ли соГ т iieniH.iN! герл!!!!. 1 Ki;\i i ..iiiHTinci-iHiCM /, , и илмеияя i:oи.Иппи-е1ггы теплооглачи oij па о: (или п/... па из>,;еняет и иелчо11ачалы1ЫЙ те[,-

ловой поток через стемку.

Л а;пз Л1й залами [1.1;1;.)лиi к следующим зависимостям для оценки цогреш11<к1е!1 пс.:ерення сшлноларьых амнератур стенки: при !>асполо-женнц ИПТ с\еле, гюказанно:; иа рие. 5Л1, о,

.-ил

1, /,

(5.53)

при расположении ИПТ по схеме, показапной па рпс. 5.11, в,

А, э(г)~г 2

n.L. - h

,2-

1.э ~- г

- 1.

(5.54)

Из (5.53) и (5.54) следу.эт раз1!ообразные частные случаи. Например, в жидких средах или при одинаковых терлюрадиациоиных характеристиках ИПТ и стенки aj а. к а,; в газовых средах обычно 1/а, > /-э/э, l/a > 2з/Яэ и т. п.

Для толстых CTCiKjK иачинас! сказываться эффект выравнивающего действия стенки па температуру ее поверхности непосредсгвенно иод ИПТ, уменьшающий величину погрешности, вычисляемую по формулам (5.53) и (5.54). Приближенный анализ этого фактора применительно к дисковым ИПТ дан в [1052].

Динамические характеристики пластинчатых ИПТ. Динамические характеристики ИПТ, применяемых для измерения температуры твердых тел, не имеют такого решающего значения, как аналогичные характеристики ИПТ, используемых для контроля температуры текучих сред. Здесь комплексно приходится учитывать взаимное влияние ИПТ и объекта. Однако для сравнительных оценок ИПТ, качественных оценок динамики измерительного процесса такие характеристики полезны.

Пусть плоский ИПТ / (рис. 5.12) с заданными теплофизическими свойствами Яд, Сэ, уэ, Оэ и толщиной Z-s используется для измерения температуры поверхности объекта 2 (массивное тело или стенка). Объект находится в теплообмене со средой с заданной температурой = const, интенсивность теплообмена определяется коэффициентом теплоотдачи а. Нестационарная температура поверхности объекта f (т) ие изменяется при наложении на него пластинчатого ИПТ. Искажение поля температур в объекте под ИПТ отсутствует при условии, что объект обладает высокой теплопроводностью (изготовлен из металла) и сохраняет ранее существовавшую равномерность поля температур,

л.л,1! ?бт1?хГГт?пл1Т ° РеДеляется его ко,

м ,г , ооьск.ом н теплообменом со средой, имеющей температуру

Т,(х. s) = K(p, S)

is) -

(5.55)

- (>) + рсЬ Р (1 - с)

: shp-pTciTfi

(5..06)

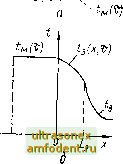Рис. 5.11. Расположение ИПТ на стенке;

а - стенка; б, в - стенка с закрепленным на левой п правой поверхности ИПТ

Рис, 5.12. Система плоский ИПТ (У) - металлическая стенка (2):

а - расположение ИПТ; б - профиль температур = aLj%, Р = j f.j, р = хИъ. Чувствительный

элемент ИПТ

располагается в плоскости л;, гдеО < л; < /-э или О < р < (см пне 5 121 В первом приближении (при малом критерии Г) азамм (5 56) можно ис пользовать передаточную функцию w . мен уэ.оо) можно ис-

К(р, S):

1-fes

4 9-49)

. (5.57) 97

поре.-ияочпмЛ коэффициент которой, опреде.тяющпй статическую norptni-иопь tlilT, имеет вид

Параметр

е ----

(1 -г);

- (1 - п)

(5.58)

(5.59)

в первом приб.тижениУ! является показателем теилсяюй иперипи n,T;(:iiii-чатого тер\юприемпика и зависит помикю конструктивных нара-тетр1я1 и ih or интенсивности теплооб.меиа ИПТ с В1!епи!ей средой, координаты (i размещения чувствительного элемента. При 1 ->- О (теплоизолированный от среды ИПТ) и сю из (5.59) получаем

8 = е I = [1 - (1 - (.)1, = е 1=. = (1 - (1 - р)-]. (5.60)

-4 S=o 2аэ

В первом приближении переход1Щя характеристика ИПТ, определяющая изменение его температуры от начальной ДО стационарной ..j. {х), Ipn = const находится обратным преобразованием выражений (5.55), (5.57):

э.пер

{X, т)-<

{X) <в

. (л:,; -/в = ст (м -<в)-

(5.01)

(5.62)

На основе (5.55) и (5.57) мегоднчсская погреннюсть Д/ измерения icm-.перагуры объекта (т) оценивается по следующим зависимостям:

Д, = 4 {X, т) - / (т) (у, - 1) / (т) - t] - у ь ;

1 -

[tsiX. т)-/в-

Шэ (х, т)

(5.63)

Более строгие опенки даются на основе передаточной функции (5.56) и ее лучших по сравнению с (5.57) аппроксимаций.

В соответствии с (5.57) частотные характеристики ИПТ имею1 вид

Л(ш) =

У 1 + 60)2

, ф (ш) = - arctg (0)8),

(5.64)

где ш - циклическая астота изменения температуры (т).

Анализ погрешностей измерения нестационарных температур металлических степок (точнее, стенок, у которых распределенпе температур близко к равномерному) с учетом экранирующего (теплоизолирующего) действия плоского термоприемника дан в работе [217]. Общая формулировка задачи для системы измеритель - стенка и ее частные решения рассмотрены в [1050].

5.6. Измерение температуры поверхности при расположении ИПТ внутри тела

В исследовательской практике и промышленных измерениях 1емпера-туры используются различные варианты разккпрения ИПТ внутри или около поверхности тела. Методические погрепнюсш в этих случаях т-за сложности анализа исследованы недосоточио подробно. Ниже npnHej(eiibi наиболее характерные расположения измерителей и расчетные соотношения для оценки погрешностей.

ПТ (термопара) в пазу на поверхности тела. Схема размещения цилиндрического ИПТ показана на рис. 5.13. Прямоугольный паз (длинная канавка), в которой располагается термопара, заполняется клеем, пастой или цементом. Иногда сверху термоэлектроды термопары дополнительно закрываются металлической фольгой. Детального решения этой задачи нет. Аналитическая и числовая оценки в предположении, что паз заполнен веществом с нулевой теплопроводностью, а ИПТ имеет пренебрежимо малое сечение и располагается по отношению к потоку на дне паза, дана в [541].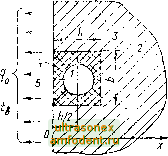

Рис. 5.13. Схе.ма расюложения ИПТ в пазу па поверхности тела:

Если теплопроводность мого тела превышает

Kg исследуе-теплопровод-

/ - термопара; 2 - исследуемое тело; 3, 4 - замазка; 5 - окружаю-1цаи среда

ность Яз замазки (зоны 3 н 4 иа рис. 5.13), систематическая погрешность измерения температуры Д( поверхности определяется смещением тер.чопа-ры на величину h/2 от поверхности и перераспределением тепловых потоков в области паза, вызванных различием Х-о, и геометрическими размерами - глубиной h и шириной b паза. Неискаженное распределение температур в теле подчиняется прямолинейной зависимости [217

Цх)=1 + --х, qo = ag(tg - te),

(5.65)

где X - расстояние от поверхности; t - действительная температура поверхности тела; - удельный тепловой поток через поверхность; а - Коэффициент теплоотдачи тела со средой; - температура окружающей среды.

В предположении, что изменение температуры на боковых стенках паза подчиняется зависимостям (5.65), распределение температур по сечению ИПТ равномерное, термопара занимает центральное положение внутри паза, уравнение для оценки статической погрешности измерения температуры поверхности имеет вид

А< = - <п = - <4 (<п ~ *в) =

Л- 1

(5.66)

11=1 + -

1 + ц (1 4- к) 2h

Ф=1+-:

(5.67)