л, 19.) ..

У 1 -т-*. ф, (Q) ~~ - arctg и.

(4.Щ (4.57)

Из выпажеиий (4 5Г) - (4 57) следусл, что амплитудно-частотная характеристика о.фсьмь.л .,и,<.11.енис амплитуды колебаний температуры тепмопппемпгка о, к амплтуде колебаний температуры среды at рассматриваемое в .твиснмости от частоты колебаний ш температуры t {%) Фазо-частотная характеристика Ч/ ( ) отражает зависимость от частоты сдвига по (bav меллу н.мДН.гт t Ы и выходным /э (т) сигналами ИИ1.

Максимальное viTCTauanne в показаниях термоприемника (т) при измерении не)иоднчески изменяющейся телнтературы среды t {%) в моменты времени, далекие oi начального, и при пулевом сигнале от возхрущающих факторов (т) - О 1ЩХ0ДИГСЯ по формуле

А......-и.(т)-а)1макс = у=Г- (4-58)

минимально допустимый период колебании 7----

При заданном Д температуры среды приближенно определяется неравенством [1050]

Т а

(4,59)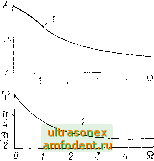

При более точных н)иближепиях для описания динамики реальных многосоставных и од1101)одиых термоприемников используют передаточные

функции второго и высших порядков по сравнению с (4.49). Возможны и практически применяются два подхода: аналитический (структурный) и расчетно-экс-периме1ггальный. В первом задается исход-пая структура ИПТ и выводятся уравнения теплообмена, решения которых определяют вид передаточных функций. Для однородных термоприемников таковыми являются уравнения (4.13), (4.17) и система передаточных функций (4.21), (4.22), из которых люгут быть найдены передаточные функции разных порядков приближения и соответственно определены приближенные уравнения взаимосвязи измеренной температуры и воздействий.

Сложные технические термоприемники, состоящие из разнородных конструктивных элементов с различными физическими свойствами, представляют систему тел, температурное поле которой является неравномерным. Чтобы математический анализ теплообмена не был чрезмерно громоздким, а исследование методических погрешностей не превратилось в самоцель, далекую от реальных измерений температуры, сложный термоприемник заменяют двумя или несколькими элементами, а затем формулируют приближенные уравнения теплообмена и решают их. Различные модели составных термоприемников, применяемых для измерения температуры текучих сред, обобщенно представлены в работе [1050], а также в публикациях [118 , 208 , 707 , 745, 746, 1049],

При исходной разбивке составного термоприемника на п элементов, каждый из которых характеризуется собственными значениями теплоемкос-

Рис. 4.7. Частотные теристики ИПТ:

/ - амплитудно-частотная: фазочастотная

харак-

ти и температуры, передаточная функция любого из элементов может быть обобщенно записана в виде

(4:60)

V (s) :

T(s)

о + OjS + + a

где коэффициенты Go.....a , ba, находятся решением исходной систе-

мы уравнений теплообмена или разложением трансцендеитпых передаточных функций в степенные ряды, если для описания теплообмена составного термоприемпика использовались уравнения в частных производных (модели ИПТ с распределенными параметрами). Структура коэ(р(ициентов, входящих в (4.60), т. е. формулы для нахождения их значеппй, определяются в процессе аналитического решения задачи. Если термоприемннк взаимодействует только с окружающей средой, а помехи отсутствуют, то в соответствии с (4,48) и используя для Yt (s) выражение (4.60), получают дифференциальное уравнение взаимосвязи измеренной (т) и действительной t (т) температур:

dt dx

+ bo.

(4.61)

которое является обыкновенным дифференциальным уравнением /i-го порядка с постоянными коэффициентами.

Расчетпо-экспериментальный подход к нахождению динамических характеристик основывается на возможности навязывания изучаемому ИПТ заранее выбранных передаточных функций (4.60), или уравнеиня (4.61), или соотношений других видов. При таком подходе структура и значения коэффициентов уравнении (4.60) и (4.61) для конкретного ИПТ не известны и подлежат экспериментальному определению подачей на вход термоприемника сигнала заданной формы и записи выходного сигнала с последующим его анализом. В практике исследования ИПТ наиболее часто иа вход подают скачкообразное воздействие, а найденную кривую изменения температуры р (т), т. е. переходную характеристику ИПТ, обрабатывают графически или с помощью ЭВМ [117, 118, 468, 754, 878, 879, 1030, 1050].

При экспериментальном исследовании динамики сложных термопри-емников вид получаемой передаточной функции и значения ее коэффициентов для одного и того же ИПТ могут быть разными при различных внешних условиях теплообмена.

Из-за инструментальных погрешностей, погрешностей обработки кривых переходного процесса, а также нестабильности условий конвективно-лучистого теплообмена передаточная функция ИПТ при ее экспериментальном определении обычно не содержит более трех-четырех коэффициентов. Если передаточная функция ИПТ определена в виде

Yt (S) =

1 +*is

(4.62)

r(s) l-fa.s + as (i + t,s) (1 + 8,s) 1,2 =4-[i ± - 402), TO уравнение переходного процесса при

Т (s) = - имеет вид (см. кривую 2 на рис. 4.6):

э.пер

= I - Bi ехр

+ fi,exp(-). (4.63)

(l.fVl)

Соответственно для амплнтудио-чапогнон и фазочастопюп ларакте-ристик получасы следующие выражения:

At (со) - ]/

1 + йсо-

(1 efco) (1 ей)) У (1 о.,со)2 ; <т,аг

И, / ft, - а, - iJoft)- 1 = arctg со -т-т-~---~

= arctg (&iCo) - arctg-

1 - a,co

(4.65)

(4.66)

4.7. Оценка случайной составляющей методической погрешности

При анализе воздействия на ИПТ входных сигналов (основного и помехосоздающих) предполагалось, что закономерности изменения их от времени заранее определены, т. е. эти воздействия являются детерминированными. В реальных условиях все входные сигналы не являются жестко заданными, и их следует считать случайными qynKHnnMH времени.

Типичный пример - изменение температуры и скорости движения потока газа или жидкости при турбулентном нестационарном режиме его течения. При турбулентном движении скорость и температура в выбранной точке потока неупорядоченно изменяются, пульсируют около некоторых средних значений. Эти пульсации наблюдаются и в том случае, когда средние скорость и температура потока постоянны во времени, т. е. течение является стационарным и изотермическим. Для турбулентного потока понятие его действительной температуры теряет свой смысл, и при ее количественном определении используют вероятностные характеристики, применяемые в теории случайных (стохастических) процессов [80, 783, 890 .

Для характеристики случайной функции 1 отображающей случайный физический процесс (например, процесс изменения температуры турбулентного потока), используют различные понятия. Наиболее употребительными из них являются следующие: 1) среднее значение (математическое ожидание) f (т) случайной функции (т); 2) дисперсия о (т) и среднее квадратичное отклонение о/ (т).

Среднее значение случайной функции f {%) представляет собой некоторая кривая /j около которой располагаются все возможные реализации случайной функции. Величины и а/ определяют отклонение, рассеивание возможных реализаций случайной функции около среднего значения

кривых (т). Если характеристики f, aj и о/ зависят от аргумента т, то случайный процессназывают нестационарным. Наиболее подробно разработана теория стационарных случайных функций (процессов), для которых среднее значение (математическое ожидание) и дисперсия не зависят от времени.

-1есмотря на случайный характер изменения физической величины между ее значениями при различных значениях аргумента (например, при раз-

личттых значениях времени или в различных точках пространства) существует определенная связь. Для оценки ?той в;мич()связи при.геняется корреляционная, пли автокорреляционная, ([уикции. Корреляционная ф.уикция стационарного случайного процесса Kf (Тц) зависит только от интервала.Тц между двумя значениями случайного процесса и может быть получена в результате осреднения по времени произведения случайных функций /сл 4л 1 ч)- Корреляционная функция Kl (т ) обладает свойством четности, положительна и уменьшается с ростом т , что отражает факт ослабления взаилюсвязи между значениями функттии f (т), разделетшых птгтервалом т . Крайние значения корреляцнопюй функции позволяют определить среднее значение, дисперсию и среднее квадратичное отклонение случайного процесса:

(4.67) (4.68)

о) = Kf (0)

Kf (оо), = YKf{0)-Kf (со),

где - среднее по времени значение функции /.j, (т), причем 7., =J,a Kf (0) и Kf (со) - значения Kf (т ) соответственно при т = О и т = оо.

Конкретная структура автокорреляционных функций находится экспериментально. В практике температурных измерений (анализ турбулентных течений, атмосферная турбулентность) для аппроксимации корреляционной функции применяют различные выражения [8, 783], из которых наиболее используемы следующие:

/ (т ) = оГи! (>о), (4.69)

Kf (Ти) = ое cos рт (х > 0), (4.70)

где Х и р - экспериментально определяемые постоянные величины.

Оценка случайной составляющей методической погрешности при измерениях может быть выполнена после исследования прохождения входного случайного сигнала через звенья всей измерительной цепи и получения характеристик случайного сигнала на выходе. В общем случае требуется детальный анализ входных случайных сигналов, учет их воздействия на динамическую характеристику ИПТ и ПВ. В зависимости от конкретных условий существенно изменяются методика и трудоемкость выполняемых оценок случайной составляющей погрешности измерений. Подробное обсуждение задач прохождения случайных сигналов через измерительные системы дано в работах [ 130, 145, 491, 675, 783, 890), а применительно к задачам термометрии - в монографии [8[.

Реальный входной сигнал / (т) можтю разделить на детерминированную /д (т) и случайную (т) составляющие и анализировать их прохождение через ИПТ раздельно:

/ () = /дет ()

/ел W-

(4.71)

Такой подход требует предварительного обоснования, однако как первое приближение может быть использован при оценке характеристик случайной составляющей сигнала на выходе ИПТ.

При указанных выше допущениях детерминированная составляющая

/дет W находится как среднее значение (математическое ожидание) / (т) =

= / (т) входного сигнала. Прохождение этого сигнала через ИПТ анализируется по обычным правилам (см. уравнения (4.8), (4.20)), в результате применения которых получают значение детерминированной составляющей температуры чувствительного элемента ИПТ Тд (т). Зная величину э.дет по уравнению (4.34) определяют систематическую составляющую методической погрешности.

Случайная составляющая рассматривается как стационарная случайная функция данного входиого снгиала, се математическое ожидание (среднее значение) равно нулю, т. е. f == 0. Дисперсия и среднее квадратич. ное значение о/ определяются заданием соответствующей корреляционной функции входного сигнала (4.69), (4.70) и соотношением (4.6,S). Среднее значение стационарной случа1П1ой .функции на выходе ИПГ равно нулю, т. е. Т (х) = 0. Взаилюсвязь дисперсий случайных составляющих выходного и входного сигналов находится по общим правилам с учето.м заданной структуры дшщмических .характеристик ИПТ.

Наиболее пюстые инженерные оценки получаются для однородных термоприемннков, имеющих передаточную функцию вида (4.49). Если случайная составляющая температуры среды Т (т) характеризуется корреляционной функцией (4.69) и имеет дисперсию of, то дисперсия на выходе ЧПТ в установившемся режиме находится по формуле [80, 1050]

1+Р8

(4 72)

Если корреляционная функция входного сигнала Г (х) имеет вид (4.70), то для ИПТ с передаточной функцией (4.49) справедливо соотношение

1+Ц8

у1

(4.73)

2 (i+pe)-fpV

Таким образом, при действии на вход ИПТ температуры среды

Т (X) = Гд (т) + Г, (X) (4.74)

на выходе ИПТ будет формироваться сигнал

Т, (X) = Г, д (X) + Гз (X). (4.75)

Детерминированная составляющая д . (т) находится в соответствии с (4.8) или (4.20). Дисперсия случайной составляющей (т) для ИПТ с передаточной функцией (4.49) находится по формулам (4.72) и (4.73) в соответствии с (4.69), (4.70).

Соотношения (4.72) и (4.73) справедливы только для стационарных линейных ИПТ, т. е. для таких ИПТ, параметры которых не изменяются под воздействием входного сигнала [248, 1050]. Отклонение от этого условия приводит к возникновению так называемых параметрических эффектов и появлению дополнительных погрешностей, носящих также случайный характер. Так, при измерении температуры турбулентного потока случайные пульсации скорости течения вызывают случййные изменения конвективной составляющей коэффициента теплоотдачи и соответственно показателя тепловой инерции ИПТ (вм. (4.31)), являющегося одним из основных параметров передаточных функций (4.21), (4.49).

Математические формулировки таких задач и анализ методических погрешностей измерения температуры сред с учетом переменности коэффициента теплоотдачи в разных приближениях рассмотрены в работах [8, 375, 1050].

Вклад в случайную составляющую выходного сигнала могут давать и не указанные выше воздействия, например, влияние электромагнитного поля на показания электрических термометров сопротивления и термопар, возникновение внутренних шумовых помех, вызванных условиями работы элементов измерителыюй системы. Учет каждого такого воздействия требует дополнительного анализа.

ГЛАВА 5

МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ ПОВЕРХНОСТИ И ВНУТРИ ТЕЛА

5.1. Погрешности измерения температуры внутри тела

Для исследования распределения температуры внутри твердых или сыпучих тел применяют ИПТ различного конструктивного оформления. Методическая погрешность при контактном измерении внутренних температур зависит от ряда факторов, важнейшими из которых являются особенность расположения термоприемника внутри тела и его ориентация относительно первоначального направления теплового потока; отличие тер.чи-ческого сопротивления термоприемника от термического сопротивления того участка тела, где размещается термоприемник; ратннца в удельных теплоемкостях и плотностях терхюприемника и исследуемого объекта.

Полный учет влияния перечисленных факторов требует совместного решения двух задач: анализа температурного поля в исследуе.мом теле при отсутствии ИПТ и изучения распределения температур в системе объект - находящийся в нем ИПТ. Провести этот анализ в форме, удобной для последующего инженерного расчета, удается лишь в ограинченпых случаях при ряде допущений относительно выбора тепловы.х люделсн тела и ИПТ. Поэтому для уменьшения методической погрешности измерения желателыю соблюдать следующие требования: 1) объем и размеры термоприемпика выбирать минимaльиын; 2) теплофизические свойства ИПТ по возможности приближать к теплофизическим свойствам исследуемого тела; 3) ИПТ располагать в изотермической области, что особенно важно при исследовании поля температур в непосредственной близости от границ тела..

Цилиндрический ИПТ в толще массивного тела. Если в теле существует заданное одномерное температурное поле t (г) с первоначальным градиентом b = dtfi(z)ldz, К/м, то цилиндрический ИПТ с радиусом R с оью, параллельной изотермам поля (г), будет искажать это поле [217, 397]. Величина температурного возмущения внутри ИПТ определится зависи.\ю-стью

At (2) = <э (г) - t, (г) =

к + к

Ьг,

(5.1)

где2 - координата; и - коэффициенты теплопроводности объекта

Качественно ход разности А< Jг) внутри и вне ИПТ вдоль оси z при э < показан на рис. 5.1, о. Если чувствительный элемент цилиндрического ЙПТ, например электроды термопары или нить термометра сопротивления, расположен в центре О сечения ИПТ или равномерно заполняет всю область /, что характерно для полупроводниковых ИПТ, то погрешность измерения температуры Л,- = О, т. е. показания ИПТ (2) полностью соответствуют температуре тела t (2) на уровне г = 0. При наличии децентри-ровання чувствительного элемента возникают дополнительные погрешности.