ипгг

двух случаях: а) участок дна сместился вверх, б) участок дна сместился вниз. В первом случае цунами распространяется приливной волной вперед, а во втором случае - отливной волной вперед. Именно во втором случае наблюдается кратковременное отступление моря от берега непосредственно перед появлением гребня волны цунами.

Вся жизнь волны цунами может быть разделена на четыре последовательных этапа. Первый этап - зарождение волны. Второй этап - движение волны по просторам океана. Третий - взаимодействие волны с прибрежной зоной. Четвертый - обрушивание гребня волны на береговую полосу, перемещение водных масс над сушей.

О зарождении цунами мы уже говорили. Рассматривая движение цунами по океанским просторам, необходимо принять во внимание огромную длину этих волн, во много раз превышающую глубины океанов. Для волн цунами все моря и океаны являются мелкой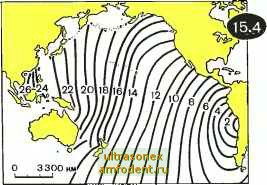

водой. Поэтому скорость распространения цунами описывается формулой (14.2): v= ]/gH . Допустим, что глубина океана равна 4 км. Подставляя в упомянутую формулу значения g=10 м/с и Н= =4000 м, получаем

1)=200 м/с=720 км/ч.

Высота и длина волны цунами (а значит, и ее энергия) зависят от силы подземных толчков, от того, насколько близко к поверхности дна находится эпицентр землетрясения, от глубины моря в данном районе. Очевидно, что

волна цунами будет тем мощнее, чем крупнее масштабы смещения дна и чем быстрее совершаются эти смещения. Все это, однако, не влияет на скорость волны цунами, которая определяется фактически только глубиной океана. В разных точках океана глубина различна; соответствующим образом будет изменяться и скорость цунами. Зная рельеф океанского дна и место зарождения цунами, можно рассчитать, через какое время волна добежит до того или иного побережья.

На рисунке 15.4 приведены полученные с использованием ЭВМ последовательные положения фронта чилийского цунами 22 мая 1960 г. Видно, что через 14 ч волна пришла на Гавайские острова и к Новой Зеландии, через 19 ч она достигла берегов Австралии, а через 22 ч берегов Японии.

Рассмотрим задачу. Как будут отличаться моменты прихода волны цунами в пункты В и С, отстоящие от очага цунами А на гООО км (рис. 15.5), если к северу от А глубина океана Н,=4 км, а к югу Н=1 км?

Обозначим расстояния \АВ\ и \АС\ через L. В пункт В волна придет через время ti - L/ZgHT, а в пункт С через время (г = L/ /gUZ Используя численные значения величин, находим: (=5000 с=83,5 мин; <2= Ю* с= 167 мин. Таким образом, в пункт С цунами придет на <2 - <i =83,5 мин позже, чем в пункт В.

Когда цунами приближается к побережью, начинается третий этап ее жизни - существенно уменьшаются скорость и длина волны, начинает расти ее высота. Предположим, что волна переместилась от линии, где глубина Я к

Я,), при

линии, где глубина Яд (Яд Скорость волны уменьшится этом на величину

Av= \fjiu- VJfh7 (15.1)

а длина волны сократится на величину

ДЛ=Г(>/77Г- /). (15.2)

Записывая последнее выражение, мы воспользовались формулой 14.4 и считали при этом, что период волны Т остается неизмен-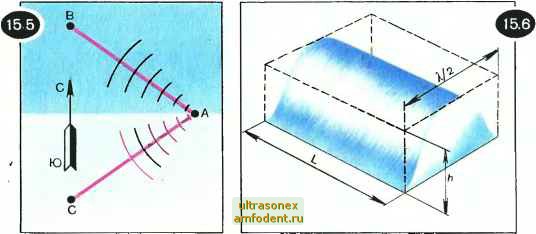

ным. Чтобы оценить увеличение высоты волны, будем рассуждать следующим образом. Выделим участок волнового фронта протяженностью L и оценим потенциальную энергию массы воды, поднятой гребнем волны, имеющим высоту h (рис. 15.6). Если бы гребень волны имел прямоугольную форму, изображенную на рисунке штриховыми прямыми, то искомая потенциальная энергия была бы равна

EmgJl. =

(15.3)

где m - масса воды в объеме гребня волны, Q - плотность воды. Но гребень волны, конечно, не имеет прямоугольной формы, поэтому вместо (15.3) запишем

E=aQLgh\

(15.4)

где а - некоторое число (очевидно, что а<;1/4). Будем полагать, что по мере перемещения с относительно глубокого места (где параметры волны есть hi и Я ) на более мелкое (где параметры волны ftg и Я-а) сохраняется величина Е, которую можно рассматривать как меру энергии, запасенной в волне. Тогда из (15.4) получаем

h\-ki=hl-k2.

(15.5)

С учетом формулы Я,= Г gH находим отсюда

hi /77, =hi fH2

и, следовательно,

h/h/Wth. (15.6)

Это соотношение известно как закон Эри - Грина.

Рассмотрим задачу. Во сколько раз изменятся скорость, длина и высота волны цунами при ее перемещении от линии, где глубина Я=5 км, к линии, где глубина N=50 м?

Обозначим параметры волны для глубины Я, через и Xf, ft а для глубины

через Oji 2> f2 В данном случае Я/Я2=100 и поэтому, согласно (15.6), /i2 ii=3,16. Исходя из того, что v= ]/gH, находим v,/v2= ]/HJH2= Ю. Аналогично для длин волн: Я./?2=10. Предположим, что вдали от берега волна цунами имела скорость 1000 км/ч, длину 10 км, высоту 2 м. При приближении к берегу, на глубине 50 м, ее скорость уменьшится до 100 км/ч, длина сократится до 1 км. а высота увеличится до 6,3 м.

Заметим, что все эти расчеты являются приближенными. В частности, они явно не годятся, когда глубина воды становится порядка нескольких метров. В этом случае уже нельзя пренебрегать трением воды о поверхность дна и, кроме того, необходимо принимать во внимание, что теперь волна стано-