дугой, если высота солнца над горизонтом превышает 42°, и не увидит дополнительной радуги при высоте солнца больше 53°. Иное дело, если наблюдатель находится в самолете: в этом случае он может увидеть радугу в виде полной окружности. Но где бы ни находился наблюдатель (на земной поверхности или над нею), он всегда есть центр ориентированного на солнце конуса с углом раствора около 42° для основной радуги и 53° для дополнительной. Почему именно 42° и 53°? На этот вопрос мы ответим позднее.

Решим задачу. Найти углы, под которыми видны вершина и основание радуги, если высота солнца Ч=20° (рассматривается желтый участок радуги).

Угловая высота вершины радуги определяется сразу из (8.1): ф=у->К=42°-20°= =22°. Чтобы найти угол а, под которым видно основание радуги, обратимся к рисунку 8.1. Из треугольника BOO,: OOJOB= =cos V- Из треугольника А О О,: OOJOA= =cos Ч. Из треугольника AOD:OA/OD= =cos а. Так как

cosy

cos42°

00, OB

00, OA OA OB

00, OA

OA OD

cosi() cos 20° Отсюда следует, что a=38°.

=0,79.

то, следовательно, cosv=cosVcosa. Таким образом,

Развитие представлений о физике возникновения радуги. Многократно наблюдая радугу, люди, естественно, давно пытались понять физику ее возникновения. В 1571 г. флетчер из Бреслау опубликовал работу, где утверждал, что наблюдатель видит радугу в результате попадания в его глаз световых лучей, каждый из которых испытал двукратное преломление в одной капле дождя и последующее отражение от другой капли дождя (рис.8.2,а). В начале XVn в. итальянец Антонио Доминико предложил иной (и, заметим, правильный) вариант прохождения светового луча к наблюдателю. Он утверждал, что достаточно рассмотреть одну каплю дождя. Изображение радуги формируется в результате того, что световой луч испытывает в капле дождя двукратное преломление и одно отражение (рис.8.2,б). Исходный световой луч А,А, входя в каплю, преломляется в точке А, затем испытывает отражение в точке В и, наконец, преломляясь.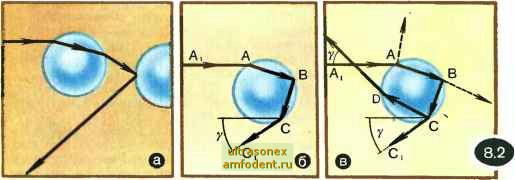

выходит из капли в точке С. В глаз наблюдателя попадает луч СС,. Он образует с исходным лучом Л, Л угол у (точнее, угол 180° - у); в резудьтате наблюдатель видит радугу под углом у к направлению падающих солнечных лучей.

Рене Декарт, развивая представления Доминико, показал, почему упомянутый выше угол у близок к 42°. Кроме того, он объяснил возникновение дополнительной радуги. Декарт исходил при этом из схемы лучей, показанной на рисунке 8.2,в. В каждой из точек А, В и С световой луч испытывает как преломление, так и отражение. Правда, луч, отраженный в А, а также луч, преломленный в В, не участвуют в формировании изображения радуги и в данном случае интереса не представляют (эти лучи показаны на рисунке штриховыми линиями). Луч, преломленный в точке С, участвует в формировании изображения основной радуги; луч, отраженный в С, выходит после преломления в точке D из капли и формирует изображение дополнительной радуги. Основную радугу наблюдатель видит под углом 7=42°, а дополнительную под углом 7=53°.

Однако ни Доминико, ни Декарт не сумели объяснить возникновение цветов радуги. Доминико, например, полагал, что световые лучи, которые проходят внутри капли наименьший путь и потому в наименьшей степени смешиваются с темнотой , дают красный цвет, тогда как лучи, проходящие наибольший путь внутри капли, в наибольшей степени смешиваются с темнотой , порождая фиолетовый цвет. Подобные наивные (и, разумеется, совершенно оши-

бочные) представления о возникновении цветов при преломлении были характерны для доньютонов-ской оптики. Они основывались на теории цвета Аристотеля, который утверждал, что различие в цвете связано с различием в количестве темноты, примешиваемой к солнечному (белому) цвету. Фиолетовый цвет, по Аристотелю, возникает при наибольшем добавлении темноты к свету, а красный - при наименьшем.

Исаак Ньютон доказал ложность представлений о возникновении цветов из смешения темноты и белого света. Выполнив целый комплекс блестящих оптических опытов с призмами, Ньютон пришел к выводу, что никакого цвета не возникает из белизны и черноты, смешанных вместе, кроме промежуточных темных , что количество света не меняет цвета , что свет состоит из лучей всех цветов не только по выходе из призмы, но даже тогда, когда он еще не дошел до призмы, до всякого преломления . Ньютонова теория цветов позволила полностью объяснить физический механизм образования радуги.

В Лекциях по оптике Ньютона обобщены полученные ранее результаты и дано следующее исчерпывающее объяснение возникновения радуги: Из лучей, входящих в шар, некоторые выходят после одного отражения, другие после двух отражений; есть лучи, выходящие после трех и даже большего числа отражений. Поскольку дождевые капли очень малы относительно расстояния до глаза наблюдателя, так что физически могут считаться за точки, то не стоит совсем рассматривать их величины, а только

углы, образуемые падающими лучами с выходящими. Там, где эти углы наибольшие или наименьшие, выходящие лучи более сгу-щены. Так как различные роды лучей составляют различные наибольшие и наименьшие углы, то лучи, наиболее плотно собира-юш,иеся у различных мест, имеют стремление к проявлению собственных цветов (курсив наш.- Автор).

Основная информация в крайне лаконичной форме заключена в строках, выделенных нами курсивом. Весь дальнейший разговор о радуге будет фактически посвящен разъяснению этих строк. Напомним, что Лекции по оптике были написаны в 70-х годах XVII в.; опубликованы они были в 1729 г.

Ход светового луча в капле дождя. Пусть на дождевую каплю радиусом R падает пучок параллельных световых лучей. Назовем прицельным параметром луча отношение =q/R, где q - расстояние

от данного луча до параллельной ему прямой, проходящей через центр капли. Будем сначала полагать, что все . световые лучи имеют одну и ту же длину волны, т. е. будем рассматривать преломление и отражение света в капле без учета его дисперсии. Капля имеет форму шара. Сферическая симметрия капли приводит к тому, что все лучи с одинаковым прицельным параметром (эти лучи показаны на рисунке 8.3) будут описывать внутри капли аналогичные траектории и будут выходить из капли под одним и тем же углом к первоначальному направлению. Траектория каждого луча лежит в плоскости, проходящей через исходное положение данного луча и параллельную ему прямую, проведенную через центр капли. Поэтому будем рассматривать двумерную задачу, изображая ход световых лучей в упомянутой плоскости.

На рисунке 8.4 показан ход луча, имеющего прицельный параметр q/R. Легко видеть, что q/R= sina, где а - угол падения луча