ным), рассмотрим однородное магнитное поле и выясним, как будет двигаться в таком поле заряженная частица.

Предположим, что частица массой m с положительным зарядом е влетает в такое поле со скоростью V, направленной перпендикулярно силовым линиям поля

(vA-B). Обозначим через S плоскость, перпендикулярную к сило-

вым линиям поля. Частица будет двигаться в этой плоскости по окружности под действием силы

Лоренца F, играющей роль центростремительной силы. В этом нетрудно убедиться, обратившись к рисунку 10.4,а. Сила Лоренца изображена на рисунке для двух точек траектории частицы. Всякий раз для выявления направления этой -силы надо мысленно повора-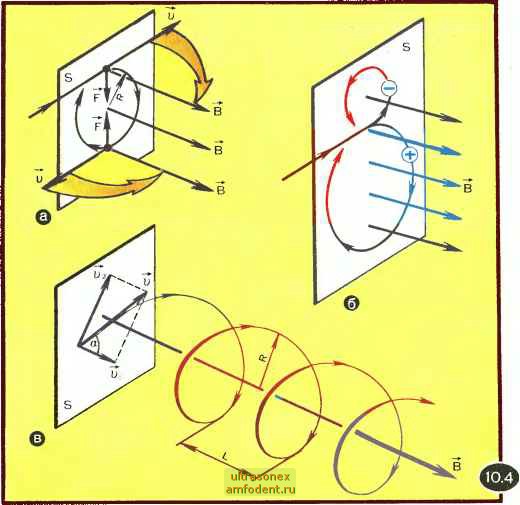

чивать вектор скорости кк вектору магнитной индукции В и применять описанное ранее правило буравчика. Из (10.1) и (10.2) следует, что в рассматриваемом случае F=evB. Радиус окружности частицы R (его называют rupo-радиусом] найдем, воспользовавшись вторым законом Ньютона, который в данном случае можно записать в виде

evB=m-

(10.4)

(здесь, напоминаем, есть мо-

дуль центростремительного ускорения).

Из (10.4) получаем

j=.rnv/eB. (10.5)

Рисунок 10.4,а относился к частице с положительным зарядом;

в этом случае сила Лоренца F совпадает по направлению с векторным произведением F/e = vy(B. Если у частицы отрицательный заряд, то, как уже отмечалось, векторы F и F/e будут направлены в противоположные стороны. Такая частица совершает движение по окружности вокруг силовых линий поля в направлении, обратном по отношению к направлению движения положительно заряженной частицы. На рисунке 10.4,6 сравниваются движения частицы с положительным и частицы с отрицательным зарядом. Если смотреть навстречу силовым линиям поля, то положительно заряженная частица совершает поворот по часовой стрелке, а отрицательно заряженная против часовой стрелки.

Рассмотрим задачу. Чему равен гирорадиус протона, если известно, что гирорадиус электрона, имеющего такую же энергию,

есть Re = b м? Масса протона в 1840 раз больше массы электрона.

Обозначим через т и М массы электрона и протона соответственно, а через V,. и Vp их скорости, в соответствии с (10.5) запишем для электрона

Re=mVe/eB

И для протона

R = Mv/eB.

Отсюда видно, что

R М Vp

т V с

(10.61

Так как энергии электрона и протона одинаковы, то mvl = Mvl и, значит,

fp/y, = /т /М.

Подставляя это соотношение в (10.6), находим

Rp/Re= \/М/т .

(10.7)

Учтем, что М/т = 1840 и Re = 5 м. В результате получаем Rp = 2\5 м.

Теперь предположим, что частица с положительным зарядом е,

массой т и скоростью v влетает в однородное магнитное поле

(магнитная индукция В) под углом а к силовым линиям; этот угол называют питч-углом. Разложим вектор V на две составляющие Vi и U2 - соответственно вдоль силовых линий (ui = ucosa) и перпендикулярно к ним (u2==ysina).

Вектор V] параллелен вектору В,

и поэтому v\XB = 0\ значит, вдоль силовых линий поля частица будет перемещаться с постоянной скоростью (скоростью и,). В то же время она будет совершать обороты вокруг силовых линий со

скоростью в соответствии с

(10.5) радиус оборотов (гирора-диус частицы) есть

Таким образом, частица будет двигаться в однородном магнитном поле по спиральной траектории, которая как бы намотана на силовые линии поля. Эта спираль изображена на рисунке 10.4,в, где R и L - соответственно радиус и шаг спирали.

Рассмотрим задачу. Если бы частица двигалась в плоскости, перпендикулярной к силовым линиям однородного магнитного поля (т. е. если бы а=90°), то в этом случае ее гирорадиус был бы Ra = 5 м. Известно, что частица влетела в поле под углом а=45° к его силовым линиям. Найти радиус и шаг спирали, описываемой частицей.

В рассматриваемом случае

Vt = V2=-

где V - модуль скорости частицы; Радиус

спиральной траектории частицы А; ==

= {ти/еВ)/ fT=--Чтобы найти шаг спи-

рали, надо определить период Г обращения частицы вокруг силовой линии. Он определяется по формуле

... 2nR

(10.8)

Учитывая, что

находим

2л;йо

Подставляя этот результат в формулу для шага спирали (/.=у,Г), получаем

/. = Л(/2 Ло.

Итак, радиус и шаг спиральной траектории частицы описываются в данном случае

выражениями:

Л = Яо/)/2~, /. = Я)/2~Ло-

С учетом того, что Ro = 5 м, находим отсюда R=3,5 м, /.=22 м.

Особенности движения заряженной частицы в неоднородном магнитном поле. На рисунке 10.5 сопоставляются картины силовых линий для однородного (а) и неоднородного (б) магнитных полей. Магнитная индукция неоднородного поля, изображенного на рисунке 10.5,6, возрастает в направлении оси z; по мере увеличения Z силовые линии все более сближаются ( сгущаются ).

Предположим, что в рассматриваемое неоднородное магнитное поле влетает положительно заряженная частица со скоростью и, ориентированной в плоскости S перпендикулярно к оси z (рис. 10.6,а). Вектор магнитной индукции в точке А на рисунке разложим на две составляющие - перпендикулярную к плоскости S

(составляющая fi,) и лежащую в плоскости S (составляющая В)-Последняя составляющая перпендикулярна к оси z; ее наличие связано с неоднородностью поля (в однородном поле, показанном на рисунке 10.5,а, такой составляющей нет).

Сила F=evxB,

лежит в плоскости S. В этом нетрудно убедиться, если мысленно

совершить поворот от вектора v к вектору B и воспользоваться

правилом буравчика. Сила \ заставляет частицу совершать обо-