на поверхность капли. Так как треугольники АОВ и ВОС равнобедренные, то AOAB=Z.ABO и АОВС== Z.BCO. Угол падения равен углу отражения, поэтому Z.ABO= =/LOBC. Обозначим все эти углы через Р (см. рисунок). Картина хода луча симметрична относительно прямой 00. В точках А и С световой луч, преломляясь, поворачивается на угол а-р (в каждой из этих точек). В точке В световой луч поворачивается на угол 180° - 2р. Таким образом, выходящий из капли луч СС, оказывается повернутым относительно исходного направления на угол 2(а -р) + (180° -2Р) = 180° + 2а - -4р. Это есть угол 180°-7. oiтcюдa следует, что

7=4р -2а.

(8.2)

Заметим, что на рисунке 8.4 не показаны лучи, отраженные в Л и С, а также луч, преломленный в В. Эти лучи не представляют интереса в данном случае.

Выразим угол у через прицельный параметр луча, падающего на каплю. Закон преломления в точке А имеет вид: sina/sinp= =п, Tfe п - показатель преломления воды. Используя (8.2), получаем

-2а sin а

Вспоминая замечание Ньютона, что размеры капли несущественны и она может считаться за точку , отметим: соотношения (8.3) и (8.4), являющиеся основными для дальнейшего рассмотрения, содержат только углы (углы 7 и а) и, разумеется, показатель преломления п.

Рассмотрим задачу. При каких значениях прицельного параметра световой луч выйдет из капли строго назад?

Итак, требуется найти значения параметра I, при которых 7=0. Полагая в (8.5)

7 = 0, получаем 2 arcsin --= arcsin I

или, иначе, sin arcsin (~)]=5-

Учитывая, что sin2v = 2sinv )/1 - sin\, находим отсюда

Уравнение (8.6) имеет два корня. Первый корень очевиден; 5i=0; второй корень есть

(8.7)

sin-

(8.3)

Подставляя в (8.7) п=4/3, получаем 2= =0,994. Заметим, чо обычно используемое для воды значение показателя преломления 4/3 соответствует лучам, попадающим в желтую часть спектра.

ИЛИ, иначе.

=arcsln(i!).

Итак,

7=4 arcsin(!i)-2а (8.4) или, с учетом того, 4TOsina= = E, 7=4 arcsin-i--2 arcsin . (8.5)

Наибольший угол между падающим на каплю и выходящим из нее лучами. Из рассмотренной выше задачи следует, что по мере увеличения прицельных параметров лучей от нуля до единицы угол 7 растет от нуля до некоторого максимального значения, а затем уменьшается, снова обращаясь в нуль при =0,994 (для желтых лучей). Важно найти максимальное значение угла 7,

поскольку, как отмечал Ньютон, там, где эти углы наибольшие или наименьшие, выходящие лучи более сгущены .

Решим в связи с этим задачу. Найти максимальное значение угла между падающим на каплю и выходящим из нее лучами. При каком прицельном параметре реализуется этот угол? Показатель преломления принять равным 4/3.

Сразу оговоримся: эта задача под силу лишь тем, кто знаком с началами математического анализа. Остальным придется при-неть на веру получаемый в задаче численный результат и ограничиться рассмотрением приводимых ниже рисунков 8.5 и 8.6. Итак, надо найти максимум функции определяемой выражением (8.5). Для этого функцию v() дифференцируют и затем приравнивают производную нулю. Производная функция v() есть

Приравняв ее нулю, получим уравнение: п /1 - {l/nf =2 .

Решая это уравнение, находим значение 5, при котором функция v(e) принимает максимальное значение. Нетрудно найти, что

(8.8)

При п=Л/3 имеем =0,861. Подставляя (8.8) в (8.5), получаем выражение для максимального угла между падающим на каплю и выходящим из нее лучами:

Vma.x = 4arcsin(-i \/ - (8.9)

- 2arcsin у---.

При п=4/3 имеем Vmax=42°02.

На рисунке 8.5 представлена для желтых лучей зависимость угла Y от прицельного параметра . На дождевую каплю падают лучи со всевозможными (от О до 1) прицельными параметрами. Они выходят из капли под разными углами Y- Естественно, что наблюдатель увидит более яркими те лучи, которые будут иметь меньшую расходимость. Такими являются лучи.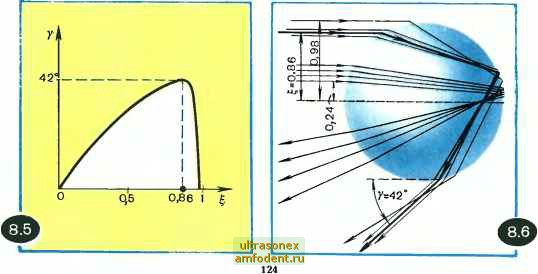

попадающие в район максимума кривой, изображенной на рисунке 8.5, т. е. лучи, для которых у=А2°. По выражению Ньютона, именно эти лучи более сгущены .

Сгущение выходящих из капли лучей вблизи угла у=42° хорошо демонстрирует рисунок 8.6, на котором показаны рассчитанные траектории световых лучей, характеризующихся разными прицельными параметрами (траектории получены для п=4/3).

Теперь легко понять, почему радуга имеет вид дуги, наблюдаемой под углом 42° к прямой линии, проходящей через наблюдателя и солнце. Для простоты будем полагать, что солнце находится у самой линии горизонта и что завеса дождя имеет вид отвесной стены, плоскость которой перпендикулярна к направлению солнечных лучей. На рисунке 8.7 дан разрез плоскостью, совпадающей с плоскостью поверхности, на которой стоит наблюдатель: MN - завеса дождя, О - наблюдатель, О, - противосолнечная точка. На рисунке заштрихована область, в пределах которой в глаз наблюдателя попадают лучи, каждый из которых испытал в какой-то капле дождя отражение и двукратное преломление; вне этой области такие лучи к данному наблюдателю не попадают. Лучи, приходящие к наблюдателю от дождевых капель, находящихся справа от С и слева от D, заметно ослаблены из-за относительно большой расходимости. Наиболее яркими будут лучи, приходящие к наблюдателю от границы заштрихованной области, т. е. от капель вблизи точек С и D, поскольку расходимость этих лучей минимальна. Итак, если бы в спектре солнца была представлена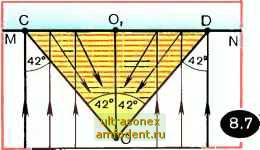

лишь одна длина волны, наблюдатель увидел бы радугу в образе узкой светящейся дуги. При этом небо под дугой будет представляться наблюдателю несколько более светлым, чем небо над дугой.

Капли дождя, конечно, не висят в воздухе неподвижно, а довольно быстро падают вниз. Поэтому та или иная капля участвует в формировании изображения радуги лишь в течение очень короткого промежутка времени - тогда, когда направление на нее от наблюдателя составляет с направлением 00, угол, близкий к 42°. Затем капля выходит из игры, но на смену ей приходят новые и новые капли. Капли сменяют друг друга быстро, так что глаз наблюдателя не улавливает происходящей смены; в результате наблюдатель видит неподвижное изображение радуги. Аналогичным образом мы видим какое-либо неподвижное изображение на экране кино, несмотря на то, что каждую секунду совершается смена 24 кадров. В этом смысле радугу можно назвать своеобразным небесным кино .

Объяснение возникновения дополнительной радуги. Мы рассмотрели ход лучей в дождевой