

 |
 |
|
Главная страница Физика природных явлений На рисунке 14.7 изображена зависимость и от Я, для глубокой воды. При л>2 см эта зависимость описывается формулой (14.1), а при Я,<1 см - формулой (14.3). Тот факт, что скорость волны изменяется с ее длиной, в значительной мере определяет неупорядоченность и изменчивость картины волн на глубокой воде. Одни волны догоняют другие, волны сливаются друг с другом и волны распадаются, волны складываются в фазе и волны складываются в про-тивофазе - в итоге создается впечатление общей неразберихи. Взаимодействие волн друг с другом приводит к тому, что одна волна оказывается непохожей на другую; время от времени возникают особо высокие волны. Что же касается волн на мелководье, то эти волны, независимо от своей длины, бегут с одной и той же скоростью. Поэтому картина волн вблизи берега становится упорядоченной. Движение частиц в волне. В главе 12 мы встречались с продольными и поперечными волнами. В продольной волне, напоминаем, частицы среды движутся вперед и назад по отношению к направлению волны, создавая чередующиеся сжатия и разрежения; таковы звуковые волны Б воздухе. В твердых телах, наряду с продольными, распространяются также поперечные звуковые волны. В них частицы среды совершают колебания поперек направления распространения волны. На первый взгляд волна на поверхности воды представляется поперечной. Но это не так. Достаточно посмотреть на рисунок 14.8, чтобы сообразить: частицы воды не могут перемещаться только по вертикалям. Это означало бы, что слой 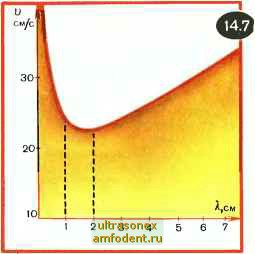 воды толщиной Н должен был бы оказаться растянутым по линии АА на величину Д и, напротив, сжатым по линии ВВ на ту же величину. Вода, очевидно, не может так сильно растягиваться и сжиматься; хорошо известно, что вода практически несжимаема. Вспомним движение пробки на волне. Как мы уже отмечали, попадая на гребень, пробка движется 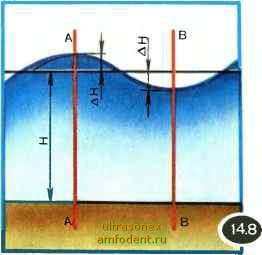 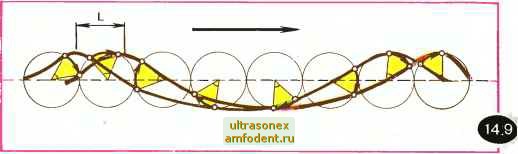 вперед, а соскальзывая затем в ложбину волны, движется назад. Итак, вперед и назад. И при этом одновременно поднимается на гребне и опускается в ложбину. В результате пробка описывает в вертикальной плоскости траекторию, которая, как оказывается, близка к окружности. Таким же образом движутся и частицы воды в волне. Следовательно, волны на поверхности воды - это не лоле-речные и не продольные волны. Каждая частица в такой волне движется приблизительно по окружности в вертикальной плоскости, параллельной направлению распространения волны. На рисунке 14.9 зеленым цветом показан профиль волны в некоторый момент времени. На профиле выбраны восемь частиц, выделенных на рисунке маленькими кружочками. Каждая частица движется по своей окружности диаметром, равным высоте волны; движение происходит по направлению часовой стрелки. За некоторый промежуток времени каждая частица описала дугу, соответствующую углу, окрашенному на рисунке в желтый цвет. Проведем через новые положения рассматриваемых точек плавную кривую (красная кривая на рисунке). Легко видеть, что это есть профиль нашей волны, сместившийся по отноше- нию к исходному профилю на расстояние L вправо. Таким образом, мы убеждаемся, что движение частиц по окружностям действительно согласуется с волновым движением. Мы все время говорим здесь не просто о частицах воды, а о частицах воды в волне . Что скрывается за таким уточнением? Известно, что волнение быстро уменьшается по мере погружения. Наверху, вблизи поверхности может происходить сильное волнение, а в то же самое время внизу, в глубине будет царить полный покой. Например, у К. Д. Бальмонта: На этом темном влажном дне Нет волн и нет лучей... Волнение на море затрагивает лишь приповерхностные слои воды. Поэтому и не чувствует дна волна на глубокой воде. Рассмотрим, как движутся частицы воды на разных глубинах, когда по поверхности воды бежит волна. Орбиты частиц изображены на рисунке 14.10,а. Чем дальше от поверхности воды, тем меньше радиусы окружностей, описываемых частицами. Уменьшение радиуса с глубиной происходит очень быстро. Уже на глубине в половину длины волны радиус уменьшается в 23 раза, а на глубине, равной одной длине волны, он уменьшает- ся более чем в 500 раз. Таким образом, опустившись на глубину всего в половину длины волны, мы практически уже не ош,утим волнения. Поэтому понятие глубокой воды можно спокойно применять, начиная с глубин порядка длины волны. Все сказанное о движении частиц в волне верно, как говорят, в первом приближении. При более строгом рассмотрении этого вопроса выясняется, что центры окружностей, описываемых частицами, вовсе не неподвижны, а медленно перемещаются по направлению волны. Действительное движение частиц следует рассматривать как наложение двух движений: быстрого кругового и медленного прямолинейного. Получается, что частицы движутся в действительности не по замкнутым траекториям, а по разомкнутым. Так как скорость кругового движения существенно больше скорости прямолинейного, то поэтому и возможно в первом приближении говорить об окружностях и использовать рисунки 14.9 и 14.10. Однако сделанное уточнение относительно перемещения центров окружностей достаточно принципиально. Оно указывает на то, что приповерхностные водяные массы все же перемещаются в направлении волны, хотя, конечно, с гораздо меньшей скоростью, нежели сама волна. Именно это перемещение вод масс позволяет жителям побережий собирать всевозможные дары моря. Ранее мы не раз подчеркивали появление у морских волн острых гребней. Оказывается, что заострение гребней связано с перемещением частиц воды по направлению волны. Наконец, заметим, что указанное направление есть необходимое условие уменьшения радиуса орбит частиц воды по мере погружения. Рассмотрим задачу. Показать, что уменьшение радиусов орбит частиц с глубиной предполагает разомкнутость круговых траекторий частиц, что связано с их перемещением по направлению волны. В этом нетрудно убедиться, если воспользоваться рисунком 14.10,6. На нем изображены две окружности: 1 - орбита А-частицы и 2 - орбита В-частицы. Радиус второй орбиты 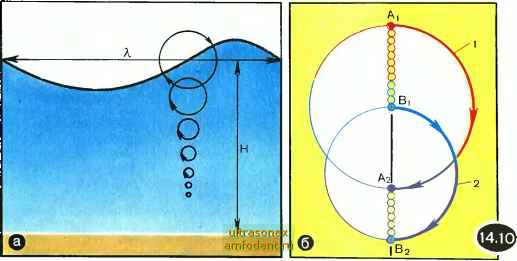
|
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |