ках 10.1,г,ж,з полярное сияние имеет достаточно четко выраженную ленточную форму. Сияние на рисунке 10.1, е можно рассматривать как наложение друг на друга лучистой и ленточной форм.

В заключение приведем весьма обстоятельное описание картины полярного сияния, составленное советским полярником Г. А. Ушаковым: Небо пылало. Бесконечная прозрачная вуаль покрыла весь небосвод; какая-то неведомая сила колебала ее. Вся она горела нежным лиловым светом. Кое-где показывались яркие вспышки и тут же бледнели, как будто на мгновенье рождались и рассеивались облака, сотканные из одного света. Сквозь вуаль ярко светили звезды. Вдруг вуаль исчезла. В некоторых местах еще раз вспыхнули лиловые облака. Какую-то долю секунды казалось, что сияние погасло. Но вот длинные лучи, местами собранные в яркие пучки, затрепетали бледно-зеленым светом. Вот они сорвались с места и со всех сторон, быстрые как молнии, метнулись к зениту, на мгновение замерли в вышине, образовали огромный сплошной венец, затрепетали и потухли .

Где и когда они наблюдаются.

Предположим, что мы смотрим на нашу планету из космоса, находясь где-то над Северным полюсом.

Полярные сияния будут образовывать светящийся венчик над планетой, овалом окружающий полюс. Этот овал и есть та область, где полярные сияния наблюдаются наиболее часто. Ее называют овальной зоной полярных сияний или, иначе, авроральной

зоной. Фактически полярные сияния происходят в этой зоне все время. Овал зоны сияний смещен в ночную сторону земного шара. Это хорошо видно на рисунке, помещенном в левом нижнем углу на с. 141. Овальная зона сияний выделена на рисунке желтым цветом. На дневной стороне (стороне, обращенной к Солнцу) зона простирается от широты 75° до широты 80°, а на ночной стороне примерно от 60° до 70°. Положение овала зоны фиксировано по отношению к Солнцу. В течение суток Земля совершает оборот под этим овалом. Наряду с зоной сияний вблизи Северного полюса существует такая же зона в Южном полушарии - вблизи Южного полюса.

Приведенные данные о размерах и положении овальной зоны полярных сияний относятся к периодам спокойного Солнца - когда солнечная активность находится на среднем уровне. При повышении солнечной активности размеры зоны сияний существенно увеличиваются. После особенно сильных возмущений на Солнце зона сияний может расшириться настолько сильно, что охватит средние и даже нижние широты - вплоть до экватора. При этом заметно возрастает интенсивность свечения сияний.

Что такое полярное сияние. От

Солнца во все стороны, и в частности к Земле, непрерывно распространяются не только волны электромагнитного излучения, но и потоки летящих с огромной скоростью заряженных частиц - так называемый солнечный ветер. Вторгаясь в земную атмосферу, частицы солнечного ветра (в ос-

новном электроны и протоны) определенным образом фокусируются и направляются магнитным полем Земли. Благодаря воздействию со стороны земного магнитного поля космические электроны и протоны проникают в пределах зон полярных сияний достаточно глубоко в атмосферу - вплоть до высот порядка 100 км (но не ниже!). Сталкиваясь с атомами и молекулами атмосферного воз-духа, они ионизуют и возбуждают их, в результате чего возникает свечение люминесценции, которое, собственно говоря, и есть полярное сияние.

Итак, полярное сияние - это люминесцентное свечение, возникающее в результате взаимодействия летящих от Солнца заряженных частиц (электронов и протонов) с атомами и молекулами земной атмосферы. Появление же этих заряженных частиц в определенных районах атмосферы и на определенных высотах есть результат взаимодействия солнечного ветра с магнитным полем Земли.

Физика полярных сияний достаточно сложна. Чтобы разобраться в ней, читатель должен иметь представление о том, как движутся заряженные частицы в магнитных полях, какова структура магнитного поля Земли, что такое люминесценция. Поэтому, прежде чем переходить к физике сияний, остановимся сначала на указанных вопросах.

Сила Лоренца; векторное пронзведенне двух векторов. Предположим, что частица с зарядом е движется в магнитном поле. Пусть в некоторый момент времени

скорость частицы есть иГ а магнитная индукция в этот момент в точке простран-

ства, где находится частица, есть В. В рассматриваемый момент времени на частицу будет действовать со стороны

магнитного поля сила F, определяемая следующей формулой:

/=еО<а (10.1)

Эта формула была получена нидерландским физиком X. Лоренцом, поэтому силу 7 называют силой Лоренца.

Формула (10.1) нуждается в разъяснении. Стоящий в ней знак X означает, что вектор скорости v векторно умножается на вектор магнитной индукции В, или, иными словами, что F/e есть векторное произведение векторов v и В. Расскажем, что это такое - векторное произведение двух векторов.

Пусть имеются два вектора (а и Ь), составляющие друг с другом угол ф, и пусть S - плоскость, проходящая через эти векторы (рис. 10.3,а). Векторно умножая вектор а на вектор Ь, мы получаем новый вектор (обозначим его как с), который называется векторным произведением векторов а и Ь: с = ахй. Этот вектор определяется так: его модуль есть

с = аЬ sin(f, (10.2)

направлен он перпендикулярно к плоскости S, причем в ту сторону, куда будет перемещаться ось винта или буравчика, который вращают в направлении

от вектора а к вектору b (в сторону меньшего угла между векторами). Предположим, что мы смотрим на плоскость S сверху так, как это изображено на рисунке 10.3,а. Поворот от вектора а к вектору b соответствует вращению против часовой стрелки. При этом буравчик будет как бы вывинчиваться из плоскости; его ось будет перемещаться вдоль себя самой от плоскости к наблюдателю. Именно в этом направлении и будет ориентирован вектор с.

Если бы мы умножали векторно не

вектор а на вектор Ь, а, наоборот, вектор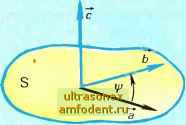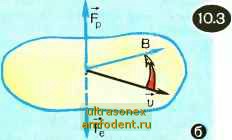

b на вектор а, то должны были бы мыс- для протона (сила F) и для электрона

(сила f,).

Скорости электрона и протона выбраны в данном случае одинаковыми.

Векторное произведение F/e, а значит, и сила Лоренца F перпендикулярны к плоскости векторов v к В. Это означает, в частности, что сила Лоренца в любой момент времени перпендикулярна к скорости частицы. Следовательно, эта сила не может производить работу. Она не может ни увеличить, ни уменьшить энергию частицы, а лишь изменяет направление ее движения. Иными словами, сила

ленно совершить поворот от 6 к а. Ему соответствует вращение по часовой стрелке, и, значит, буравчик будет как бы ввинчиваться в пространство под плоскостью S; его ось будет перемещаться от наблюдателя (вниз). Теперь векторное

произведение (пусть это будет вектор с) ориентируется не вверх, а вниз. Это означает, что с = - с или, иначе говоря.

bxa = - {axb).

(10.3)

Мы видим, что векторное произведение двух векторов меняет свой знак при перемене мест сомножителей. Это тот особый случай, когда при перемене мест сомножителей произведение меняется.

После сделанных замечаний вернемся к формуле (10.1). Теперь ясно, что вектор

F/e должен быть перпендикулярен к плоскости, проходящей через векторы v и В. Чтобы выявить одно из двух возможных направлений этого перпендикуляра, надо

мысленно совершить поворот от v к В и сообразить, куда при этом будег перемещаться ось буравчика. Если частица заряжена положительно, направление силы

Лоренца F будет совпадать с направлением векторного произведения F/e. Для отрицательно заряженной частицы векторы F и F/e будут направлены в противоположные стороны. На рисунке 10.3,6 показано, как направлена сила Лоренца

Лоренца изменяет направление вектора v, оставляя неизменным его модуль.

Движение заряженной частицы в однородном магнитном поле.

Напомним, что поле называют однородным, если его напряженность одинакова во всех точках. Силовые линии такого поля представляют собой семейство взаимно параллельных прямых. Всякое реальное поле является неоднородным, так что однородное поле - это идеализация. Однако идеализация эта весьма полезная, поскольку в пределах достаточно малой области пространства поле практически всегда можно приближенно считать однородным. Поэтому, прежде чем переходить к магнитному полю Земли (являющемуся, разумеется, неоднород-