Fmn силы, удерживающей снег на склоне, начнет с течением времени постепенно уменьшаться. Скатывающая же сила Mg sina остается при этом, очевидно, неизменной. В результате в какой-то момент времени (он может наступить на следующие сутки или даже через несколько дней) постепенно уменьшающееся предельное значение f max становится меньше силы Mg sin а - тогда равновесие нарушается и начинается движение снега.

Почему сцепление снега с поверхностью склона может уменьшаться с течением времени? Вопрос этот непростой. По-видимому, определенную роль играет эффект, о котором мы говорили в главе 18. Напомним, что если температура внутри слоя снега понижается в направлении от грунта к поверхности снега, то в этом случае из-за перемещения водяных паров снизу вверх формируется характерная слоистая структура: вблизи грунта образуется рыхлый слой глубинного инея, а наверху, у поверхности снега, уплотненная снежная доска . В морозный день температура у поверхности снега действительно ниже, чем в его глубине, вблизи грунта. Поэтому вполне можно допустить, что уменьшение сцепления снега с поверхностью горного склона есть результат формирования придонного слоя глубинного инея. Следует, однако, заметить, что, как показали исследования, дело, по-видимому, не только в глубинном инее. Образование внутри снежного покрова ледяных зерен фирна также способствует уменьшению сцепления снега с горным склоном.

При подземных толчках, а также при стрельбе из орудий, когда

образуется достаточно мощная звуковая волна, сцепление снега со склоном понижается скачком и начинается движение снежной массы. Это есть третья из отмечавшихся выше групп лавин. Возникновение лавины от не слишком сильных звуков возможно, очевидно, лишь когда снежная масса, что называется, висит на волоске , т. е. когда сила Mg sin а всего лишь на ничтожную величину меньше, чем fmai.

Совсем нетрудно объяснить теперь и последнюю, четвертую группу лавин. Оттепель приводит к таянию, снег насыщается водой, вода опускается внутри снежного слоя вниз и течет по склону горы, образуя тонкую прослойку между снегом и грунтом. Эта прослойка действует как смазка - она весьма эффективно уменьшает сцепление снега с горным склоном. И хотя по мере таяния снега скатывающая сила Mg sin а уменьшается, все же предельное значение fmax силы, удерживающей снег на склоне, уменьшается еще быстрее. В результате возникает возможность образования лавины.

Итак, устойчивость снежного покрова, лежащего на склоне горы, определяется тем, насколько скатывающая сила Mgsind меньше предельного значения fmax удерживающей силы. Снег неподвижен, пока Algsina<;fmax; при этом скатывающая сила уравновешивается удерживающей силой:

Mgsin a=F.

Иногда можно встретить утверждение: снег неподвижен, пока удерживающая его на склоне горы сила больше скатывающей силы . Такое утверждение не просто ошибочно, оно абсурдно. Ведь при f>Mgsina снег должен был

бы не лежать, а двигаться с ускорением по направлению силы F, иначе говоря, двигаться вверх по склону. Необходимо подчеркнуть: удерживающая сила автоматически следует за скатывающей силой. Уменьшается скатывающая сила - уменьшается и удерживающая; увеличивается скатывающая сила - увеличивается и удерживающая. Вот только не может удерживающая сила F стать больше своего предельного значения fmax, а последнее уменьшается со временем, при оттепелях, подземных толчках и т. д. Равновесие нарушается и возникает снежная лавина, когда в силу тех или иных причин неравенство

Mg sina<f ,3,

превращается в неравенство

Mg sina>f, .

Пока

Mg&\na<.F ,

условие равновесия выполняется {Mg sin a=F). Если же

Mg&\na>F ,

то условие равновесия, очевидно, выполняться не может - ведь

Внимание! Лавина. Мы обсудили физику возникновения лавины. Значительно более сложной оказывается физика движения лавины, физика ее развития. Известно, что движение лавины может начинаться от нарушения устойчивости снежного покрова практически в точке - сдвиг одного кубического метра снега или и того меньше. Но очень быстро в движение вовлекается все больше и

больше снега - и вот в нижней части горного склона несется с оглушительным гулом в облаке белой пыли снежная масса, объем которой измеряется десятками и сотнями тысяч, а иногда и миллионами кубических метров. Скорость разогнавшейся лавины доходит до 20-50 м/с.

Какова физика столь стремительно ускоряющегося процесса? Ученые пока не могут удовлетворительно ответить на этот вопрос. Во многих странах в настоящее время начаты исследования физики развития снежных лавин. Надо подчеркнуть, что проводить подобные исследования очень сложно: опасно работать на лавиноопасном склоне, практически невозможно сколь-либо точно предугадать момент возникновения лавины, трудно и опасно выполнять те или иные измерения над низвергающейся вниз снежной массой. Фактически пока получены лишь самые первые экспериментальные данные по лавинам; многие из них еще не имеют объяснения.

Все лавины начинают свое движение либо от точки (нарушается устойчивость малого объема снега), либо от линии (нарушается устойчивость значительного пласта снега). Лавина от линии схематически показана на рисунке 20.3,а, а лавина от точки - на рисунке 20.3, б. На рисунке 20.3,а выделены три зоны: I - зона зарождения лавины, II-зона транзита, III - зона отложения снега, принесенного лавиной. Расстояние по горизонтали от линии отрыва до дальнего края зоны отложения называют дальностью выброса лавины; для небольших лавин она измеряется сотнями метров, а для крупных - километ-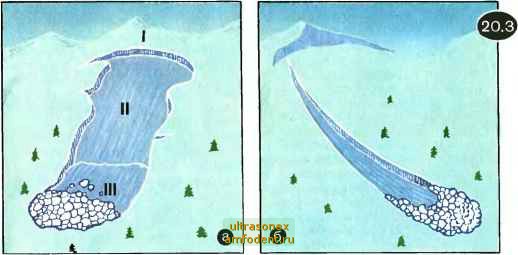

рами и десятками километров. Заметим, что лавины от точки возникают, когда поверхностные слои снега достаточно рыхлые, тогда как лавины от линии образуются при наличии снежной доски у поверхности снега. Физика развития как тех, так и других лавин фактически не исследована.

Если разогнавшаяся лавина встречает препятствие, она наносит по нему сильный удар. Мощность удара измеряют мгновенным значением давления, оказываемого снегом на препятствие в момент удара. Это давление называют ударным; оно измеряется тысячами и десятками тысяч килопас-калей (что соответствует сотням и тысячам тонн на квадратный метр). На рисунке 20.4 приведен довольно интересный график, полученный исследователями лавин на Хибинском нагорье. По вертикали на графике отложены высоты 2 точек в поперечном сечении лавины, в которых измерялось ударное давление р, а по горизонтали - отношение измеренного ударного давления к его

максимальному значению ртм (которое в данном случае составляло 1070 кПа). Оказывается, ударное давление меняется по поперечному сечению лавины. В самом низу оно небольшое, затем возрастает, достигая максимального значения на высоте 1,3 м, после чего еще быстрее уменьшается, становясь

равным -- Ртах на высоте 2 м; да-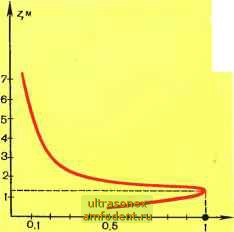

Р/Ртах