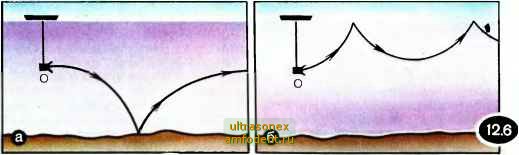Рефракция звука происходит не только в воздухе, но и в воде. Как и в воздухе, скорость звуковых волн в воде увеличивается с ростом температуры. Значит, температурная рефракция звука под водой аналогична его рефракции в воздухе.

На рисунке 12.6 показана температурная рефракция звука в воде летом (а) и зимой (б).

Летом температура воды понижается с глубиной, поэтому звуковые лучи изгибаются книзу и затем отражаются от дна. Зимой, напротив, температура нижних слоев воды выше, чем приповерхностных; в этом случае звуковые лучи изгибаются кверху и отражаются от поверхности раздела вода - воздух. Заметим, что скорость звука в воде зависит не только от температуры, но и от концентрации солей в воде. Чем больше соленость воды, тем выше (при той же температуре) скорость звука. Нетрудно сообразить, что траектория звукового луча должна быть обращена в ту сторону, где соленость воды больше.

Гидроакустики пользуются легко запоминающимся правилом: подобно жаждущему человеку, звуковой луч в морской воде всегда стремится в сторону более холодных и менее соленых слоев воды.

Когда существенна длина звуковой волны? До сих пор мы рассматривали отражение звуковых волн от стенок и протяженных поверхностей. В этих случаях длина звуковой волны несущественна (она важна лишь с точки зрения обеспечения направленности звуковых волн; чем меньше длина волны, тем легче реализовать более высокую направленность). Предположим теперь, что звук отражается от объектов, размеры которых относительно невелики, например от копны сена, камня, ствола дерева и т. д. Здесь принципиально важно соотношение между размерами отражающего объекта (будем характеризовать их величиной d) и длиной волны звука К. Если k<d, то звуковая волна отражается от объекта (подобно тому как она отражалась от стенки). Если Xd, то звуковая волна проходит сквозь объект, как бы не замечая его. Точно так же волны на поверхности воды проходят сквозь тонкие стебли растений, торчащие из воды. Обе ситуации иллюстрирует рисунок 12.7 (?b,<Crf; )2)- Они помогают объяснить возникновение высоких тонов в эхо-сигналах в упоминавшемся ранее примере поезда, проходящего по железнодорожному мосту. Когда мимо окна проносится очередная балка мостовой

фермы, наблюдатель воспринимает отраженные ею звуковые волны. На балку падает много звуковых волн разной частоты, однако, как мы уже знаем, отражаются лишь те, длина которых меньше диаметра балки, т. е. волны с достаточно высокой частотой. Поэтому в восгфинимаемом наблюдателем звуковом шуме и будут выделяться высокие тона.

Изображенная на рисунке 12.7 картина является упрощенной; очевидно, объект должен в какой-то мере искажать картину регулярных звуковых волн. Эти искажения становятся принципиальными, когда Xxd; в этом случае наблюдается дифракция звуковых волн на рассматриваемом объекте.

Заметим, что утверждение, будто при Kd волна не замечает объекта, не вполне верно; всегда происходит частичное рассеяние звука, при этом интенсивность рассеянной звуковой волны обратно пропорциональна (в применении к световым волнам этот результат рассматривался в главе 1 в связи с обсуждением голубого цвета неба).

Эффект Доплера. Предположим, что источник звука движется к неподвижному наблюдателю со скоростью V (рис. 12.8,а; О - источник звука, А - наблюдатель). Источник генерирует звуковую волну длиной (частота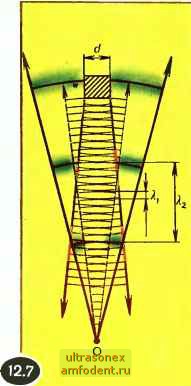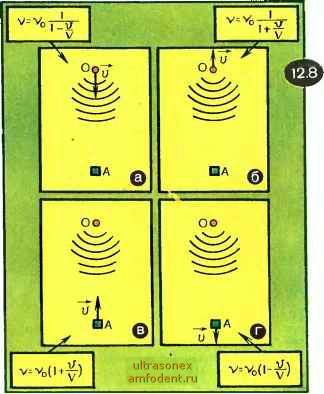

Vo=c/Xo, с - скорость звука). Вследствие движения источника звука наблюдатель будет воспринимать звуковую волну иной длины (иной частоты). В самом деле, пусть в момент времени =0 от источника к наблюдателю отправилась область сжатия. Следующая область сжатия отправится к наблюдателю в момент ,=l/vo; т. е. через промежуток времени, равный периоду колебаний. За это время источник света пройдет по направлению к наблюдателю путь v/vq) в результате расстояние между первой и второй областями сжатия окажется меньше на величину u/vq. Это означает, что наблюдатель зарегистрирует волну длиной

>,= >,o-JL . (12.5)

Переходя от длин волн >i, и >i,o к соответствующим частотам v и Vo (X=c/v; Xo=c/vo), преобразуем (12.5) к виду

c/v={c - v)/vq.

Таким образом, наблюдатель будет воспринимать звуковую волну с частотой

V = Vo

\-v/c

(12.6)

Если бы источник звука двигался со скоростью и не к наблюдателю, а от него (рис. 12.8,6), то в этом случае наблюдаемая частота описывалась бы выражением

v = Vo

\ + v/c

(12.7)

(предлагаем читателю самому убедиться в этом).

Рассмотрим теперь случай, когда источник звука покоится, а движется со скоростью v наблюдатель. Если наблюдатель движет-

ся по направлению к источнику (рис. 12.8,в), он будет регистрировать частоту

V = Vo(l+).

(12.8)

При движении наблюдателя в обратную сторону (рис. 12.8,г) будет зарегистрирована частота

v=vo(l-7). (12.9)

Результаты (12.8) и (12.9) приводим без вывода.

Зависимость регистрируемой наблюдателем частоты звука от скорости, с которой наблюдатель и источник звука сближаются друг с другом или, напротив, удаляются друг от друга, и составляет содержание эффекта Доплера в акустике (он был теоретически установлен в 1842 г. австрийским физиком К. Доплером). Когда источник звука движется к наблюдателю (или наблюдатель движется к источнику), частота звука, который слышит наблюдатель, повышается; см. (12.6) и (12.8). Когда источник звука движется от наблюдателя (или наблюдатель движется от источника), частота звука понижается; см. (12.7) и (12.9). Это, очевидно, необходимо принимать во внимание, рассматривая эхо-сигналы от движущихся объектов.

Полезно заметить, что при и-Сс можно приближенно принять:

1 - и/с

= \ + v/c; = l-v/c.

В этом случае соотношение (12.6) переходит в (12.8), а соотношение (12.7) в (12.9). В результате оказывается безразличным, источник