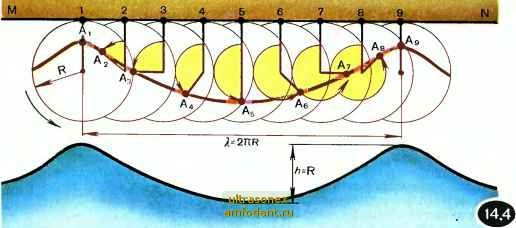ны, хотя и близок к трохоиде, тем не менее отличен от нее. В частности, он имеет меньшую крутизну, более пологую ложбину.

Скорость волны зависит от скорости ветра и длительности его воздействия на волну, причем скорость волны всегда меньше скорости ветра. Создается впечатление, что ветер как бы гонит волну, разгоняет ее. Между прочим, именно так обычно и говорят. Забегая вперед, заметим, что такое представление неверно с физической точки зрения. При постоянном ветре скорость установившихся волн составляет 0,8 от скорости ветра. Свежий ветер силой 5 баллов (такой ветер хорошо ощущается рукой, он качает тонкие стволы деревьев) имеет скорость около 10 м/с. Скорость сильного ветра силой 8 баллов (ломаются ветви и сучья) доходит до 20 м/с. Таким образом, волна может перемещаться довольно быстро - со скоростью порядка 10 м/с и более. При этом важно иметь в виду, что стремительный бег волн отнюдь не означает, что столь же стремительно переносит-

ся вещество, в данном случае вода. Бросьте в волну пробку и понаблюдайте за ней. Когда под пробкой проходит гребень, она устремляется вместе с ним вперед, однако тут же соскальзывает с него, отстает и, попадая в ложбину волны, начинает двигаться назад, пока ее не подхватит следующий гребень. Затем все повторяется. Впрочем, повторяется не полностью: всякий раз пробка смещается немного вперед.

Именно так и ведут себя частицы воды; волна бежит вперед, а водная масса совершает перемещения на одном месте , слегка смещаясь по направлению движения волны.

До сих пор мы рассматривали морские волны вдали от берега там, где море достаточно глубоко (позднее мы уточним, что означает глубоко ). Теперь обратимся к волнам на мелководье с плавно поднимающимся дном, т. е. к волнам в непосредственной близости от берега. Здесь мы видим существенно иную картину. При очень слабом ветре волны лижут кромку

берега, то набегая на нее, то отступая назад. Ветер крепчает - и волны начинают накатываться на берег, с шумом обрушиваясь, разбиваясь на мириады брызг и покрывая кромку берега пеной. При еще более сильном ветре картина прибоя становится более впечатляющей. Вблизи линии берега вырастают высокие волны с белыми гребнями (буруны). Они с грохотом опрокидываются на берег, выбрасывая на него потоки воды и обильную пену (рис. 14.5).

В картине морских волн у берега следует выделить две основные черты. Во-первых, подходя к берегу, волны становятся выше и в то же время короче, т. е. резко возрастает крутизна волн. Опытные моряки легко определяют мели и подводные рифы по особенно высоким волнам, возникающим над ними. Увеличение крутизны этих волн делает их неустойчивыми, их гребни начинают разрушаться, покрываясь белыми шапками пены. Буруны - верный признак мелководья. Во-вторых, при подходе к берегу (как и при прохождении над подводным рифом) качественно изменяется профиль волны. На глубоких местах профиль волны всегда симметричен относительно вертикальной плоскости, проходящей через верхнюю точку гребня. Теперь же такой симметрии нет.

Верхняя часть гребня смещается вперед сильнее, чем нижняя часть; Б результате волна как бы опрокидывается вперед, обрушиваясь на берег. Как образно сказал один из исследователей морских волн, волна встает на дыбы, как только почувствует почву под ногами, т. е. дно, а затем летит кувырком, разбиваясь на прибрежной отмели или рифах .

Все это хорошо видно на рисунке 14.2,в.

Дополнительно заметим, что, приближаясь к берегу, волны замедляют свое движение. Кроме того, их движение явно упорядочивается. Вдали от берега картина волн может быть весьма неупорядоченной, однако в непосредственной близости от берега мы наблюдаем регулярные волны, ориентированные, как правило, параллельно линии берега.

Скорость волн на глубокой и мелкой воде. Пусть Я - глубина, т. е. расстояние от поверхности воды до дна (имеется в виду поверхность воды в спокойном состоянии). Если Я Л, а тем более если НЖ, то говорят о глубокой воде. Если же Я<С (на практике часто используют условие Н<СХ/10), то говорят о мелкой воде. На глубокой воде волна распространяется, не чувствуя дна; в волнении участвует лишь приповерхностный слой воды толщиной не более половины длины волны. Иное дело волна на мелкой воде. Теперь в движение вовлекается вся масса воды, волна чувствует дно; ее скорость зависит от глубины. Скорость волны на глубокой воде описывается формулой

(14.1)

а на мелкой воде

v= /glT. (14.2)

Здесь g - ускорение свободного падения.

Рассмотрим задачу. Исходя из размерности физических величин показать, что скорость волны на глубокой воде должна быть пропорциональна /р.Прежде всего, сообразим, какие величины могут входить в формулу для скорости волны. Таких величин четыре: длина волны X глубина водоема Н, плотность воды Q, ускорение свободного падения g (величину g следует принимать во внимание по той причине, что сила тяжести игржет роль возврищаюгцей силы для колебаний водной поверхности). Учитывая, что рассматривается глубокая вода, сразу исключим глубину Н; ведь в данном случае волна не чувствует дна, так что величина Н не может влиять на ее скорость. Из трех оставшихся величин (X, Q, g) надо обржзовать величину, имеюгцую размерность скорости. В размерность плотности Q входит масса; размерности же остальных величин, включая и скорость, массы не содержат. Следовательно, величину q тоже надо исключить. В итоге остаются две величины: Х и g. Единственная комбинация из этих величин, имеюгцая размерность скорости, есть, очевидно, /gk . Итак, исходя только из обгцих физических соображений и учитывая размерности величин, мы получили формулу (14.1) с точностью до безразмерного множителя )/1/2л .

Из формулы (14.1) следует важный вывод: на глубокой воде скорость волн зависит от их длины. Более длинные волны бегут быстрее коротких. В этом, кстати говоря, нетрудно убедиться, бросив камень в воду. От брошенного камня побегут кругами волны. Первыми достигнут берега более длинные волны (рис. 14.6).

Внимательный читатель может вспомнить, что ранее, говоря о вол-

нах ряби, мы утверждали нечто противоположное. Мы говорили, что быстрее бегут более короткие волны. Дело в том, что формулы (14.1) и (14.2) относятся к не слишком коротким волнам, а именно к волнам, длина которых больше нескольких сантиметров. Если же длина волны оказывается меньше примерно 2 см (а именно таковы волны ряби), то в этом случае необходимо принимать во внимание поверхностное натяжение воды. Такие волны называют капиллярными, для них роль возвращающей силы при колебаниях поверхности играет сила поверхностного натяжения (по сравнению с ней влияние силы тяжести становится несущественным). Пусть о - коэффициент поверхностного натяжения; он измеряется в Н/м. Скорость капиллярной волны описывается формулой

и=/2до/дл.

(14.3)

Заметим, что для капиллярньгх волн величина g, являющаяся как бы представителем силы тяжести, никакой роли не играет; несущественна для них и величина Н - ведь для столь мелких волн любая вода глубокая. Остаются три величины: о, q, к. Единственная комбинация этих величин, имеющая размерность скорости, есть /о/дЯ,.