Пример четвертый: GN 1; CN = 5; СТ = 4; TR = = 6.

Значения, присваиваемые целочисленным переменным, совпадали с приведенными выше.

Далее были определены логические ветви программы, проверяемые в каждом из описанных выше примеров, а также наборы входных данных, активизирующие каждую ветвь.

В первом примере присваиваемое переменной GN значение О вызывает проверку ветви (GN. NF. 0.) первым условным оператором IF; результат проверки оценивается как ложь и осуществляется переход к выполнению второго оператора IF. Переменной GN присваивается значение 5, а переменной СТ - значение 4; результат проверки ветви (CN. LT. СТ) оценивается как ложь . Затем внутренней переменной IE присваивается значение 1 и выполняется четвертый оператор IF, где результат проверки (IE. NE. 1) оценивается как ложь , далее выполняются все последующие операторы вплоть до оператора RETURN. Таким образом, рассмотренный логический путь проходится при значении входной переменной ,GN = О и при значениях CN, больших или равных значению переменной СТ. Заметим, что действительная переменная TR и ни одна из целочисленных переменных не участвуют ни в каких вычислениях в этой ветви программы. Поэтому множество Gi значений входных данных, которые вызывают выполнение этой ветви программы, полностью определяется переменными GN и CN, т. е.

G,: GN==0 CN > СТ

Аналогичный анализ показывает, что в случае второго контрольного примера вьшолняется другая ветвь программы, которая определяется множеством С? значений входных данных:

Ga: GNO -

CN>TR .

Переменная СТ и целочисленные переменные не участвуют в вычислениях, относящихся к этой ветви

программы. В третьем примере проверяется третья ветвь программы, которая в свою очередь определяется множеством G3 значений входных данных:

Оз: GN О CN < СТ JA =1 JB = JD = JE = JV =

где I - любое целое число, а переменная TR не участвует ни в каких вычислениях этой ветви программы.

И наконец, в четвертом примере проверяется четвертая ветвь программы, которая определяется множеством G4 значений входных данных:

G4: GN=0 ,

CN < TR JA = I JB = I

JD = I , . .

JE = I

JV = I

причем переменная CT не участвует ни в каких вычислениях этой ветви программы.

Поскольку в исследуемой программе нет других ветвей, множество наборов входных данных Е может быть определено как объединение четырех подмножеств Gi, G2, G3, Gi-.

E = G,UG2UG3UG4.

Заметим, что Е не равно декартову произведению множеств, на которых принимают свои значения входные переменные, поскольку эти значения ограничиваются соотношениями, установленными при определении подмножеств Gy, и в силу того, что некоторые переменные входят не во все Gy.

В каждом контрольном примере используются различные Gy и инициируется выполнение разных ветвей программы. Одновременное использование всех Gy позво.пяет проверить все ветви программы, причем.

каждая из ветвей проверяется только в одном примере.

Для программы Л может быть построена логическая диаграмма проверок ветвей Вг:

Bi: gn.ne.o. В2: cn.lt.ct

В3: cn.lt.tr

В4: ie. ne. I

п выделены сегменты программы S-:

Sj: IE

S2: S3:

ie ie ie je ki km

= 0 = 0

= je+ i ==jd 2

kr =3

kb =ja

ke =jb

jv =jv + ki

kg!=i

return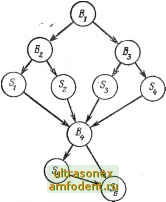

Анализируя приведенную диаграмму, можно прийти к выводу, что программа А имеет 8 логических путей, однако в действительности проходятся только 4