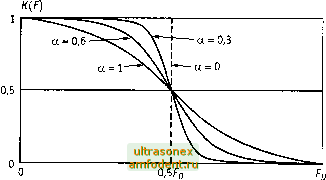Рис. 17.4. Амплитудно-частотная характеристика ФНЧ типа приподнятый косинус для различных значений а

символьные искажения, которые вызываются наложением друг на друга откпиков фильтра. Таким образом, комплексная огибающая на интервале действия к-го дибита будет зависеть от вида последовательности из / предыдущих дибит. Значение / зависит от соотношения полосы фильтра и скорости передачи.

Для минимизации межсимвольных искажений используются ФНЧ со специальными импульсными характеристиками, которые обеспечивают контролируемый уровень межсимвольных искажений. К таким фильтрам относятся фильтры Найквиста, импульсная характеристика которых пересекает нулевой уровень с периодом равным половине длительности дибита, а амплитудно-частотная (АЧХ) имеет нечетную симметрию относительно частоты среза по уровню 0,5, при этом частота среза ФНЧ /ср = 1/2То. Таким образом, независимо от формы входной последовательности в определенные моменты времени с периодичностью следования дибитов сигнал отклика фильтра будет определяться только одним дибитом. Варианты формы АЧХ фильтров Найквиста показаны на рис. 17.4. Представленные АЧХ характеризуются дополнительным параметром а, который определяет крутизну АЧХ в переходной области и скорость затухания боковых всплесков импульсной характеристики фильтра. Широко распространена форма АЧХ фильтра Найквиста в виде приподнятого квадрата косинуса

К(со) =

я(1-а)

при О со я(1-а)/Го,

, при

я(1-а) nh + a)

,(17.6)

при со> я(1-а)/7о

hiTo) 1,0

-0,2

Рис. 17.5. Импульсные отклики фильтра Найквиста (а) и корень квадратный из АЧХ фильтра Найквиста (б)

где коэффициент а характеризует степень округления спектра. Форма отклика такого фильтра (17.6) на единичный импульс

hit) = TD

S\n{nt/TD )

cosjant/Tp)

(17.7)

Форма отклика системы передачи на единичный импульс при а - 1 приведена на рис. 17.5 а и б. На рис. 17.4 частота Найквиста

сос=2яГс=2я, Fc~ = , (17-8)

где 7р - длительность дибита (рис. 17.5); Fd - тактовая частота следования дибитов.

Поскольку в сквозном тракте модулятор-демодулятор сигнал проходит через два последовательно включенных ФНЧ, то сквозная АЧХ тракта Кт = КуКг. Поэтому для обеспечения требуемой формы сквозной АЧХ необходимо, чтобы К = К2= #7 где Kj, Кг - АЧХ фильтров в модуляторе и демодуляторе.

Модуляция GMSK. В системах радиодоступа также используется гауссовская манипуляция с минимальным сдвигом ММС (Gaussian IVIinimum Shift Keying - GIVISK) (рис. 17.6). Этот метод представпяет собой частотную манипуляцию, при которой несущая частота дискретно - через интервалы времени, кратные периоду 7 битовой мoJy-лирующей последовательности, принимает значения

4=0+/4,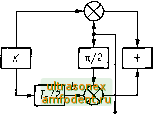

S V

COSCOq

71/2

Модулятор ФМ-4

С057СГ/2Г

Рис. 17.6. Структурные схемы модуляторов: а-ФМ-4; б-ММС

где fo ~ центральная частота используемого частотного канала, а F=1/r - частота битовой последовательности. Разнос частот

= {н -fa)/2~ минимально возможный, при котором обеспечивается ортогональность колебаний частот f и на интервале Т длительности одного бита; при этом за время Г между колебаниями частот f и 4 набегает разность фаз, равная я/2. Таким образом, термин минимальный сдвиг в названии метода модуляции относится, в указанном выше смысле, к сдвигу частоты. Поскольку модулирующая частота в этом случае равна F/2 , а девиация частоты - F/4, индекс частотной модуляции составляет т = (F/4)/(F/2) =0,5.

Термин гауссовская в названии метода модуляции соответствует дополнительной фильтрации модулирующей битовой последовательности относительно узкополосным гауссовским фильтром; именно эта дополнительная фильтрация отличает метод GMSK от метода MSK (Minimum Shift Keying - манипуляция с минимальным сдвигом).

Метод MSK иногда рассматривают как метод квадратурной фазовой манипуляции со смещением (OQPSK), но с заменой прямоугольных модулирующих импульсов длительностью 2Г полуволновыми отрезками синусоид или косинусоид (со5я/27). в методе MSK входная последовательность битовых импульсов модулятора разбивается на две последовательности, состоящие соответственно из нечетных и четных импульсов, и модулированный сигнал (выходной сигнал модулятора) на протяжении очередного п-го бита определяется выражением, зависящим от состояния текущего п-го и предшествующего (п - 1)-го бита:

s(f) = ±со5(я?/2Г)со5соо{+ sin(nf/2r)sin(Oof = = ±cos{(x)at±nt/2T), (п-т <пТ.

(17.9)

Здесь соо =2яо - центральная частота канала, а знаки плюс или минус определяются модулирующей импульсной последовательностью.

Из выражения (17.9) следует, что текущая фаза модулированного сигнала

9(f) = Wo±irf/2r,

т.е. набег фазы на интервале Годного бита

Аф + я/2,

а мгновенная частота, как производная от фазы

(0(0 = d[(p{t)]/dt = (Оо±п/2Т = 2n{f, ±F/4), т.е. мгновенная частота принимает одно из двух значений - f или f, постоянное на протяжении бита.

Таким образом, изменение знака начальной фазы во второй части выражения (17.9) означает переход от к 4 или обратно. Изменение же общего знака выражения (17.9), эквивалентное изменению начальной фазы на я/2, позволяет сохранить непрерывность фазы при

изменении частоты.

Временные диаграммы работы модулятора минимальным сдвигом приведены на рис. 17.7, где vit) - входной цифровой сигнал с дли-

.2Г -то Т 2Т 37 AT ЪТ бГ 77 8Г

Рис. 17.7. Временные диаграммы при формировании сигналов ММС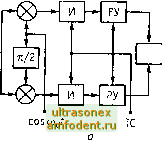

cos {Kt/2T)cos coof гЧН~

V Z

5in(7tt/27)sincoof о

Рис. 17.8. Структурные схемы демодуляторов: а-ФМ-4; б-ММС

тельностью символа Т; второй и третий графики дают соответственно последовательности нечетных ait) и четных bit) бит входной последовательности, причем длительность каждого бита равна 2Г; четвертый и пятый графики показывают форму модулирующих сигналов двух квадратурных каналов J и Q, получаемых как произведения функций ait) и bit) соответственно на квадратурные низкочастотные сигналы sin{nt/2T) и cos(nf/2r). Обратим внимание на скачкообразные изменения фазы этих сигналов (в моменты изменений знаков ait) и bit)).

Окончательный модулированный сигнал согласно первой части выражения (17.9) получается как результат перемножения модулирующих сигналов квадратурных каналов с соответствующими несущими sin(cogf) и cos((Bof) и суммирования полученных произведений. Описанный принцип построения модулятора MSK поясняется блок-схемой рис. 17.6 (пока без учета первого блока - гауссовского фильтра G). Подчеркнем, что эта схема таюке служит лишь для иллюстрации принципа работы модулятора. Введение гауссовского фильтра приводит к сужению главного лепестка и снижению боковых лепестков спектра на выходе модупятора, чем обеспечивается допустимый уровень помех по смежным частотным каналам.

Структурные схемы демодуляторов приведены на рис. 17 8. Для работы когерентных демодуляторов на приемной стороне необходимо иметь опорное напряжение, синфазное с приходящим сигнапом со5(юо0 и тактовую частоту (ТС), выделенную из приходящего сигнала.

В заключение раздела отметим, что методы модуляции л/4 DQPSK и GMSK оказываются сопоставимыми по частоте битовой ошибки (BER), хотя первый из них обеспечивает нескопько более высокую эффективность испопьзования полосы частот в расчете на 1 бит передаваемой информации.

17.2. Борьба с влиянием многолучевого распространения

Испопьзуемые в сетях радиодоступа дециметровые радиоволны слабо огибают препятствия, т.е. распространяются в основном по прямой, но испытывают многочисленные отражения от окружающих объектов и подстилающей поверхности. Одним из следствий такого многолучевого распространения является более быстрое, чем в свободном пространстве, убывание интенсивности принимаемого сигнала с расстоянием. Другое следствие - замирания и искажения результирующего сигнала. Именно эти эффекты мы и рассмотрим несколько подробнее.

При многолучевом распространении область существенных отражений ограничивается обычно сравнительно небольшим участком в окрестности абонентской станции - порядка нескольких сотен длин волн, т.е. порядка нескольких десятков или сотен метров. При движении подвижной станции эта область перемещается вместе с ней таким образом, что подвижная станция все время остается вбпизи центра обпасти. При спожении нескопьких сигнапов, прошедших по разным путям и имеющих в точке приема в общем спучае различные фазы, результирующий сигнал может быть как несколько выше среднего уровня, так и заметно ниже, причем провалы, или замирания сигнала, образующиеся при взаимной компенсации сигналов вследствие неблагоприятного сочетания их фаз и амплитуд, могут быть достаточно глубокими. Искажения результирующего сигнала, или межсимвольная интерференция, имеют место в том случае, когда соизмеримые по амплитуде и противопопожные по фазе пучи отпичаются по разности хода на время, соизмеримое с дпительностью символа.

Колебания уровня (замирания) принимаемого сигнапа практически всегда имеют две составпяющие - быструю и медпенную. Быстрые замирания, явпяющиеся прямым спедствием многопучевого распространения, описываются релеевским законом распределения и потому их иногда называют релеевскими замираниями. Диапазон изменений уровня сигнала при быстрых замираниях может достигать 40 дБ, из которых примерно 10 дБ - превышение над средним уровнем и 30 дБ - провапы ниже среднего уровня, причем более глубокие про-вапы встречаются реже, чем менее глубокие. При неподвижном абонентском аппарате интенсивность принимаемого сигнапа также изменяется из-за рефракции (искривпения траектории лучей). При перемещении подвижной станции периодичность флуктуации в пространстве составляет около полуволны, т.е. порядка 10-15 см в линейнЬй мере. Период флуктуации во времени зависит от скорости перемещения подвижной станции и изменения градиента диэлектрической проницаемости тропосферы: например, при скорости 50 км/ч период фпуктуаций составпяет около 10 мс, а при 100 км/ч - около 5 мс. Час-